giá trị nhỏ nhất và giá trị lớn nhất của hám số y= sinx+cos/2sinx-cox +3 lần lượt là:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
2 tháng 9 2017
Xét − sin x + 2 cos x + 4 = 0
Ta thấy − 1 2 + 2 2 < 4 2 nên phương trình vô nghiệm.
Do đó − sin x + 2 cos x + 4 ≠ 0 .
Như vậy, y = 2 sin x + cos x + 3 − sin x + 2 cos x + 4
⇔ y − sin x + 2 cos x + 4 = 2 sin x + cos x + 3
⇔ sin x 2 + y + cos x 1 − 2 y + 3 − 4 y = 0
Để phương trình có nghiệm thì 2 + y 2 + 1 − 2 y 2 ≥ 3 − 4 y 2
⇔ 5 y 2 + 5 ≥ 16 y 2 − 24 y + 9
⇔ 11 y 2 − 24 y + 4 ≤ 0
⇔ 2 11 ≤ y ≤ 2
Chọn đáp án D.
CM
9 tháng 12 2018
Đáp án A
Ta có: y = cos x + 2 sin x + 3 2 cos x − sin x + 4
⇒ y 2 cos x − sin x + 4 = cos x + 2 sin x + 3
⇔ 2 + y sin x + 1 − 2 y cos x = 4 y − 3 1
PT (1) có nghiệm ⇔ 2 + y 2 + 1 − 2 y 2 ≥ 4 y − 3 2
⇔ 11 y 2 − 24 y + 4 ≤ 0 ⇔ 2 11 ≤ y ≤ 2
Suy ra M = 2 m = 2 11 ⇒ M . m = 4 11
CM
1 tháng 1 2018
Chọn A
↔ (2-y)sinx + (1+2y)cosx= 3y-1(*)
Sử dụng điều kiện để phương trình (*) có nghiệm suy ra -1/2 ≤ y ≤ 2
CM
14 tháng 12 2019
Đáp án D.
Ta có y ' = c osx ⇒ y'=0 ⇔ c osx=0 ⇔ x= π 2 + k π k ∈ ℤ ⇒ x 0 = π 2 ∈ − π 6 ; 5 π 6 .
Suy ra y − π 6 = − 1 , y π 2 = 2 , y 5 π 6 = 1 ⇒ M = 2 m = − 1 .
CM
17 tháng 11 2017
Đáp án B
Ta có: y' = cosx trên đoạn - π 2 ; - π 3 hàm số y = sinx đồng biến.
Lại có sin - π 2 = - 1 ; sin - π 3 = - 3 2 vậy giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = sinx trên đoạn - π 2 ; - π 3 lần lượt là - 3 2 ; - 1 .
CM
25 tháng 6 2017
Đáp án B
Vì 
nên tập giá trị của hàm số là tập hợp các giá trị của y để phương trình 
có nghiệm.
Sử dụng điều kiện có nghiệm của phương trình 
suy ra được 
vậy m = -1 và 
CM
14 tháng 11 2017
Chọn B
Vì sinx-cosx+3>0 nên tập giá trị của hàm số là tập hợp các giá trị của y để phương trình (1-y)sinx+(y+1)cosx=(1+3y) có nghiệm.
Sử dụng điều kiện có nghiệm của phương trình A.sinx+B.cosx=C. Vậy m = -1 và M=1/7
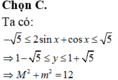
\(y=\dfrac{sinx+cosx}{2sinx-cosx+3}\Rightarrow2y.sinx-y.cosx+3y=sinx+cosx\)
\(\Leftrightarrow\left(1-2y\right)sinx+\left(y+1\right)cosx=3y\)
Theo điều kiện có nghiệm của pt lượng giác bậc nhất:
\(\left(1-2y\right)^2+\left(y+1\right)^2\ge9y^2\)
\(\Rightarrow2y^2+y-1\le0\)
\(\Rightarrow-1\le y\le\dfrac{1}{2}\)