Tìm x
2x+1_2x=32
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KH
16 tháng 5 2021
\(\left|\dfrac{1}{2}x+3\right|=\dfrac{2}{5}\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{2}x+3=\dfrac{2}{5}\\\dfrac{1}{2}x+3=-\dfrac{2}{5}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{2}x=-\dfrac{13}{5}\\\dfrac{1}{2}x=-\dfrac{17}{5}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{26}{5}\\x=-\dfrac{34}{5}\end{matrix}\right.\\ \Rightarrow S=\left\{-\dfrac{26}{5};-\dfrac{34}{5}\right\}\)
16 tháng 5 2021
`|1/2x+3|=2/5`
`+)1/2x+3=2/5`
`<=>1/2x=-13/5`
`<=>x=-26/5`
`+)1/2x+3=-2/5`
`<=>1/2x=-17/5`
`<=>x=-34/5`
Vậy `x=-26/5` hoặc `x=-34/5`
PT
1
PT
1
CM
24 tháng 9 2018
Ta có:
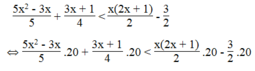
⇔ 20 x 2 – 12x + 15x + 5 < 20 x 2 + 10x – 30
⇔ 20 x 2 – 12x + 15x – 20 x 2 x – 10x < -30 – 5
⇔ -7x < -35
⇔ x > 5
Vậy tập nghiệm của bất phương trình là {x|x > 5}
A
3
XO
24 tháng 7 2020
b) Để \(\frac{2}{3\left|x-1\right|+4}\)đạt GTLN
=> 3|x - 1|+ 4 đạt giá trị nhỏ nhất
mà 3|x - 1| \(\ge0\forall x\)
=> 3|x - 1| + 4 \(\ge\)4
Dấu "=" xảy ra <=> x - 1 = 0
=> x = 1
Vậy GTLN của \(B=\frac{1}{2}\Leftrightarrow x=1\)
LT
0
27 tháng 2 2021
2x+/x/=3x ( / / là giá trị tuyệt đối nha bạn )
/x/=3x-2x
/x/=x
Do giá trị tuyệt đối của bất kì số nguyên nào đều không bao giờ là số nguyên âm nên x phải lớn hơn -1
\(\Rightarrow x\in N\)
27 tháng 2 2021
`2x+|x|=3x`
`=>|x|=3x-2x`
`=>|x|=x`
Sử dụng tính chất `|A|=|A|<=>A>=0`
`=>x>=0`
Vậy với `x>=0` thì `2x+|x|=3x`
\(2^{x+1}-2^x=32\)
\(2^x\cdot2^1-2^x\cdot1=32\)
\(2^x\cdot\left(2^1-1\right)=32\)
\(2^x\cdot\left(2-1\right)=32\)
\(2^x\cdot1=32\)
\(2^x=32\)
\(2^x=2^5\)
\(\Rightarrow x=5\)
Vậy x=5.
2x+1 - 2x = 32
2x . 21 - 2x .1 = 32
2x . ( 2 - 1 ) = 32
2x = 25
=> x = 5
Vậy x = 5