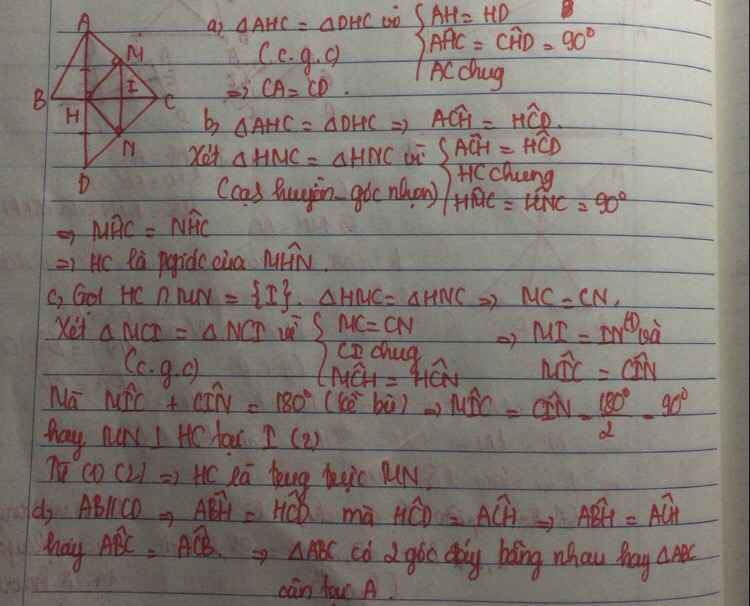Cho tam giác MNQ vuông tại M. Vẽ MI vuông góc QN.
a) Chứng minh góc MNI = IMQ
b) Vẽ NK là tia phân giác của góc MNQ, vẽ QK là tia phân giác của góc MQN. Tính góc NKQ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 4 2022
-Kẻ đg phân giác thì có liên quan gì đến điều cần c/m?
-△AMN và △NMQ có: \(\widehat{MAN}=\widehat{MNQ}=90^0\); \(\widehat{N}\) là góc chung.
\(\Rightarrow\)△AMN∼△NMQ (g-g) \(\Rightarrow\dfrac{MN}{MQ}=\dfrac{AN}{NQ}\Rightarrow NA=\dfrac{MN.NQ}{MQ}\Rightarrow NA^2=\dfrac{MN^2.NQ^2}{MQ^2}\Rightarrow\dfrac{1}{NA^2}=\dfrac{MQ^2}{MN^2.NQ^2}\Rightarrow\dfrac{1}{NA^2}=\dfrac{MN^2+NQ^2}{MN^2.NQ^2}\Rightarrow\dfrac{1}{NA^2}=\dfrac{1}{NQ^2}+\dfrac{1}{MN^2}\)
3 tháng 12 2021
1: Xét ΔHAC vuông tại H và ΔHDC vuông tại H có
CH chung
HA=HD
Do đó: ΔHAC=ΔHDC
Suy ra: CA=CD
25 tháng 12 2021
1: Xét ΔCAD có
CH là đường cao
CH là đường trung tuyến
Do đó: ΔCAD cân tại C
hay CA=CD
25 tháng 12 2021
1: Xét ΔCAD có
CH là đường cao
CH là đường trung tuyến
Do đó: ΔCAD cân tại C
hay CA=CD
17 tháng 2 2022
a: Xét ΔAMB và ΔANC có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó: ΔAMB=ΔANC
Suy ra: AM=AN
b: Xét ΔAIM vuông tại I và ΔAKN vuông tại K có
AM=AN
\(\widehat{IAM}=\widehat{KAN}\)
Do đó: ΔAIN=ΔAKN
Suy ra: AI=AK
