tam giác ABC cân tại A ,gọi DE theo thứ tự là trung điểm của AB,AC a,xác định dạng tứ giác BDEC b,cho biết BC=8cm.tính HC=HD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Kẻ \(EH\perp BC\) tại \(H.\)
a)Ta có: D là trung điểm của AB
............. E là trung điểm của AC
Do đó: ED là đường trung bình của \(\Delta ABC\)
\(\Rightarrow ED\)//\(BC\)
\(\Rightarrow BDEC\) là hình thang
Mà \(\widehat{B}=\widehat{C}\)(vì \(\Delta ABC\) cân tại \(A\))
\(\Rightarrow BDEC\) là hình thang cân.

\(\Delta\)ABC có: DA=DB(gt)
EA=EC(gt)
=> DE là đường trung bình của \(\Delta\)ABC
=> DE//BC
Xét tứ giác BDEC có: DE//BC
=> Tứ giác BDEC là hình thang
Mà:^B=^C (gt)
=> Tứ giác BDEC là hình thang cân
b)Vì DE là đường trung bình của tam giác ABC
=>\(DE=\frac{1}{2}BC=\frac{1}{2}\cdot8=4\)

Đáp án cần chọn là: C
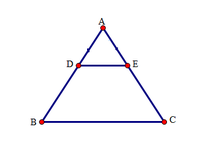
Tứ giác BDEC có DE // BC nên tứ giác BDEC là hình thang.
Lại có A B C ^ = A C B ^ (vì tam giác ABC cân tại A) nên BDEC là hình thang cân

Đáp án cần chọn là: C
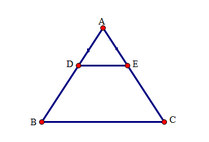
Tứ giác BDEC có DE // BC nên tứ giác BDEC là hình thang.
Lại có A B C ^ = A C B ^ (vì tam giác ABC cân tại A) nên BDEC là hình thang cân

a) Vì D, E lần lượt là trung điểm của AB và AC nên DA=DB, EA=EC \(\Rightarrow\)DE là đường trung bình của tam giác \(\Rightarrow\)DE//BC\(\Rightarrow\)tứ giác BDEC là hình thang.
Lại có BD=EC (AB=AC, AD=AE) suy ra BDEC là hình thang cân
a) Dễ dàng c/m được AD = BD = AE = CE
=> tg ADE cân tại A => \(\widehat{D_1}=\frac{180^0-\widehat{A}}{2}\)
C/m tương tự ta có \(\widehat{B_2}=\frac{180^0-\widehat{A}}{2}\)
=> góc D1 = góc B2
mà 2 góc này ở vị trí đồng vị => AE // BC => BDEC là hình thang
Mặt khác tg ABC cân tại A => góc B2 = góc C => BDEC là hình thang cân
b) đề chắc yêu cầu tính DE :v
Dễ thấy DE là đường trung bình của tam giác ABC
=> DE = 1/2 BC
=> DE = 8/2
=> DE = 4 ( cm )
Vậy.....
thank you
nếu đc bạn có thể trả lời 3 câu còn lại không @Bonking