Cho hai góc kề bù xOy và yOz . Gọi Om , On lần lượt là các tia phân giác của góc xOy ; góc yOz
a) Chứng minh Om vuông góc với On
b) Lấy điểm H thuộc tia Oy . Kẻ HE vuông góc với Om ; HK vuông góc với On ( E thuộc Om ; K thuộc On ) . Chứng minh góc EHK = \(90^0\)
c) Trên nửa mặt phẳng bờ OH có chứa tia Ox , kẻ tia Ht // Ox . Ht cắt Om tại P . chứng minh HE là tia phaann giác của góc OHP
d) Gỉa sử góc 3OHP = góc 2HOx . Tính góc HOx và góc OPH

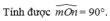
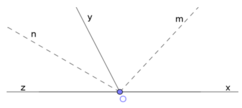

Vì \(xOy\) và \(yOz\) là hai góc kề bù
⇒ \(xOy+yOz=180^0\)
Vì tia \(Om\) là tia phân giác của \(xOy\)
⇒ \(mOy\) = \(\dfrac{xOy}{2}\)
Vì tia \(On\) là tia phân giác của \(yOz\)
⇒ \(nOy=\dfrac{yOz}{2}\)
⇒ \(mOy+nOy=\dfrac{xOy}{2}+\dfrac{yOz}{2}=\dfrac{xOy+yOz}{2}=\dfrac{180^0}{2}=90^0\)
mà hai góc này kề nhau
⇒\(mOy+nOy=mOn\)
⇒\(mOn=90^0\)
⇒\(Om\) ⊥ \(On\)
\(b,\) \(HE\) ⊥ \(Om\)
\(On\) ⊥ \(Om\)
Vì \(HK\) ⊥ \(On\)
⇒ \(HKn=90^0\)
⇒ \(HE\) // \(On\)
⇒ \(EHK=HKn\) (so le trong)
mà \(HKn=90^0\)
⇒ \(EHK=90^0\left(DPCM\right)\)
Vì xOy và yOz là hai góc kề bù
⇒ xOy+yOz=1800
Vì tia Om là tia phân giác của xOy
⇒ mOy = xOy2
Vì tia On là tia phân giác của yOz
⇒ nOy=yOz2
⇒ mOy+nOy=xOy2+yOz2=xOy+yOz2=18002=900
mà hai góc này kề nhau
⇒mOy+nOy=mOn
⇒mOn=900
⇒Om ⊥ On