cho tam giác ABC, M là trung điểm của BC . Trên tia đối của tia MA=MK
chứng minh
a)AB=CK
b)AC=AB
AB song song với BK
c)AC=BK
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 12 2021
a: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra: AB=DC
Youcho tam giác nhọn ABC, AB<AC. Gọi M là trung điểm của cạnh BC. Trên tia đối của tia MA lấy điểm D sao cho MA=MD a) chứng minh tam giác AMB=tam giác DMC b) chứng minh AB=DC c)chứng minh AB song song với CD
H9
HT.Phong (9A5)
CTVHS
16 tháng 1
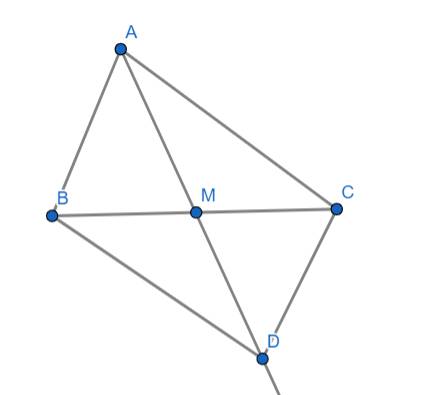
a) Xét ΔAMB và ΔDMC có:
\(AM=CM\) (gt)
\(\widehat{AMB}=\widehat{DMC}\) (đối đỉnh)
\(BM=CM\) (M là trung điểm của BC)
\(\Rightarrow\text{Δ}AMB=\text{Δ}DMC\left(c.g.c\right)\)
b) Ta có: \(\text{Δ}AMB=\text{Δ}DMC\left(cmt\right)\)
\(\Rightarrow AB=DC\) (2 cạnh t.ứng)
c) Ta có: \(\text{Δ}AMB=\text{Δ}DMC\left(cmt\right)\)
\(\Rightarrow\widehat{MAB}=\widehat{MDC}\) (hai góc t.ứng)
Mà hai góc này ở vị trí so le trong
\(\Rightarrow AB//CD\)
BẠN TỰ VẼ HÌNH NHÉ
a) Xét tam giác MCK và tam giác MBA
Có : CM = BM ( gt )
MK = MA ( gt )
Góc CMK = Góc BMA ( đối đỉnh )
Vậy tam giác MCK = tam giác MBA (c.g.c)
=> AB = CK (cạnh tương ứng )