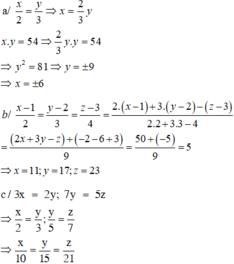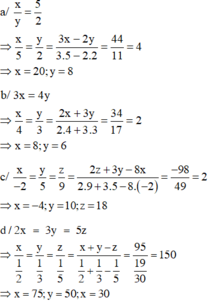X,y biết: 2x=3y và xy=54
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(2x+3y=0\)
\(\Leftrightarrow2x=-3y\)
\(\Rightarrow\frac{x}{-3}=\frac{y}{2}\Rightarrow\frac{-x}{3}=\frac{y}{2}\)
Ta có : \(\left(\frac{-x}{3}\right)^2=\frac{-x}{3}\cdot\frac{-x}{3}=\frac{-x}{3}\cdot\frac{y}{2}=\frac{-xy}{3\cdot2}=\frac{54}{6}=9\)
\(\Rightarrow\left(\frac{-x}{3}\right)=\left(\pm3\right)^2\)
\(\Rightarrow\orbr{\begin{cases}\frac{-x}{3}=\frac{y}{2}=-3\\\frac{-x}{3}=\frac{y}{2}=3\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=9;y=-6\\x=-9;y=6\end{cases}}\)
Vậy ......

a: Ta có: 3x=5y
nên x/5=y/3
Đặt x/5=y/3=k
=>x=5k; y=3k
Ta có: xy=54
\(\Leftrightarrow15k^2=54\)
\(\Leftrightarrow k^2=3.6\)
Trường hợp 1: \(k=\dfrac{3\sqrt{10}}{5}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=5k=\dfrac{15\sqrt{10}}{5}=3\sqrt{10}\\y=3k=\dfrac{9\sqrt{10}}{5}\end{matrix}\right.\)
Trường hợp 2: \(k=-\dfrac{3\sqrt{10}}{5}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=5k=\dfrac{-15\sqrt{10}}{5}=-3\sqrt{10}\\y=3k=\dfrac{-9\sqrt{10}}{5}\end{matrix}\right.\)
b: 2x=3y
nên x/3=y/2
Đặt x/3=y/2=k
=>x=3k; y=2k
\(2x^3+y^3=62\)
\(\Leftrightarrow2\cdot27k^3+8k^3=62\)
=>k=1
=>x=3; y=2

\(a,\frac{x}{10}=\frac{y}{6}=\frac{z}{21}=\frac{5x+y-2z}{50+6-42}=\frac{28}{14}=2\)
\(\frac{x}{10}=2\Rightarrow x=10.2=20\)
\(\frac{y}{6}=2\Rightarrow y=2.6=12\)
\(\frac{z}{21}=2\Rightarrow z=21.2=42\)
\(d,\frac{x}{2}=\frac{y}{3}=k\)\(\Rightarrow x=2k;y=3k\)
\(\Rightarrow ab=2k.3k=6k^2=54\)
\(\Rightarrow k^2=9\Leftrightarrow k=3\)
\(\frac{x}{2}=3\Rightarrow x=6\)
\(\frac{y}{3}=3\Rightarrow y=9\)
a) Áp dụng t/c của dãy tỉ số bằng nhau, ta có:
\(\frac{x}{10}=\frac{y}{6}=\frac{z}{21}\) => \(\frac{5x}{50}=\frac{y}{6}=\frac{2z}{42}=\frac{5x+y-2z}{50+6-42}=\frac{28}{14}=2\)
=> \(\hept{\begin{cases}\frac{x}{10}=2\\\frac{y}{6}=2\\\frac{z}{21}=2\end{cases}}\) => \(\hept{\begin{cases}x=2.10=20\\y=2.6=12\\z=2.21=42\end{cases}}\)
Vậy x = 20; y = 12; z = 42
b) Ta có: \(\frac{x}{3}=\frac{y}{4}\) => \(\frac{x}{15}=\frac{y}{20}\)
\(\frac{y}{5}=\frac{z}{7}\) => \(\frac{y}{20}=\frac{z}{28}\)
=> \(\frac{x}{15}=\frac{y}{20}=\frac{z}{28}\)
Áp dụng t/c của dãy tỉ số bằng nhau, ta có:
\(\frac{x}{15}=\frac{y}{20}=\frac{z}{28}\)=> \(\frac{2x}{30}=\frac{3y}{60}=\frac{z}{28}=\frac{2x+3y-z}{30+60-28}=\frac{125}{62}=\frac{125}{62}\)
=> \(\hept{\begin{cases}\frac{x}{15}=\frac{125}{62}\\\frac{y}{20}=\frac{125}{62}\\\frac{z}{28}=\frac{125}{62}\end{cases}}\) => \(\hept{\begin{cases}x=\frac{125}{62}.15=\frac{1875}{62}\\y=\frac{125}{62}.20=\frac{1250}{31}\\z=\frac{125}{62}.28=\frac{1750}{31}\end{cases}}\)
Vậy ...

Giải:
Ta có: \(5x-17y=2xy\)
\(\Rightarrow5x-17y=2\left(2x+3y\right)\)
\(\Rightarrow5x-17y=4x+6y\)
\(\Rightarrow11x=23y\)
\(\Rightarrow\frac{x}{23}=\frac{y}{11}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{23}=\frac{y}{11}=\frac{x-y}{23-11}=\frac{5}{12}\)
\(\Rightarrow x=\frac{115}{12};y=\frac{55}{12}\)
Vậy...
Bạn kiểm tra lại nhé, bài này mk ko chắc lắm đâu, có thể bị sai nhé