gí trị của x^3 - y^3 - 3xy biết x - y = 1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


y x \(\dfrac{1}{3}\) = 6
y = 6 : \(\dfrac{1}{3}\)
y = 18

b; 13 = (\(x-y\))3 = \(x^3\) - 3\(x^2\).y + 3\(xy^2\) - y3 = \(x^3\) - y3 - 3\(xy\)(\(x-y\))
1 = \(x^3\) - y3 - 3\(xy\)

Có: \(x^3-y^3-3xy=x^3-y^3-3xy\left(x-y\right)\) (vì x-y=1)
\(=\left(x-y\right)^3=1^3=1\)

Có : x^3+3xy+y^3
= (x^3+y^3)+3xy
= (x+y).(x^2-xy+y^2)+3xy
= x^2-xy+y^2+3xy ( vì x+y = 1 )
= x^2+2xy+y^2
= (x+y)^2
= 1^2 = 1
Vậy giá trị của biểu thức x^3+3xy+y^3 = 1
Tk mk nha
Ta có: x3+y3=(x+y)(x2-xy+y2)=1*((x2-xy+y2)=x2-xy+y2
=> x3+y3+3xy=x2-xy+y2+3xy=x22xy+y2 = (x+y)2=12=1
Đáp số: 1

c)\(x^3+3xy+y^3\)
\(=x^3+y^3+3xy=\left(x+y\right)\left(x^2-xy+y^2\right)+3xy\)
\(=\left(x^2-xy+y^2\right)+3xy\)
\(=x^2-xy+y^2+3xy\)
\(=x^2+2xy+y^2=\left(x+y\right)^2\)
\(=1^2=1\)
a) cho x+y=1. Tính giá trị biểu thức x^3+ y^3+ 3xy
b) cho x-y=1. Tính giá trị biểu thức x^3- y^3- 3xy

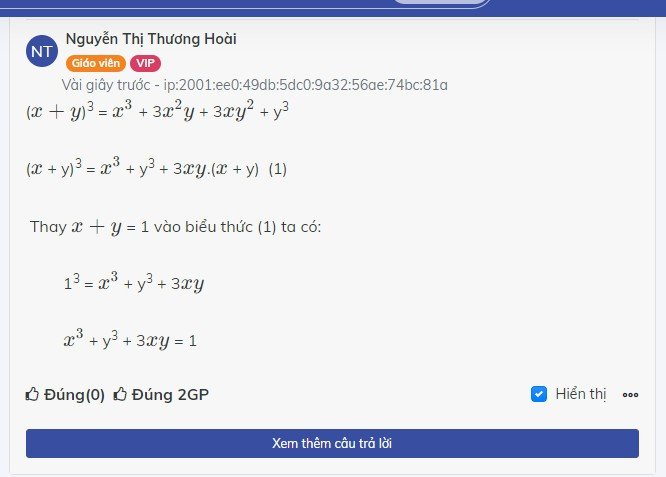
x^3+ y^3+ 3xy
=(x+y)(x^2 -xy + y^2 ) + 3xy
=x^2 -xy + y^2 + 3xy
=x^2 + 2xy + y^2
=(x+y)^2 =1
=> x^3+ y^3+ 3xy=1

cho rõ lời giải hộ tớ được không và cho cả giá trị x,y nữa
x^3-y^3-3xy
=(x-y)(x^2+xy+y^2)-3xy
=1(x^2+xy+y^2)-3xy
=x^2+xy+y^2-3xy
=x^2-2xy+y^2
=(x-y)^2=1^2=1
tick nha bn