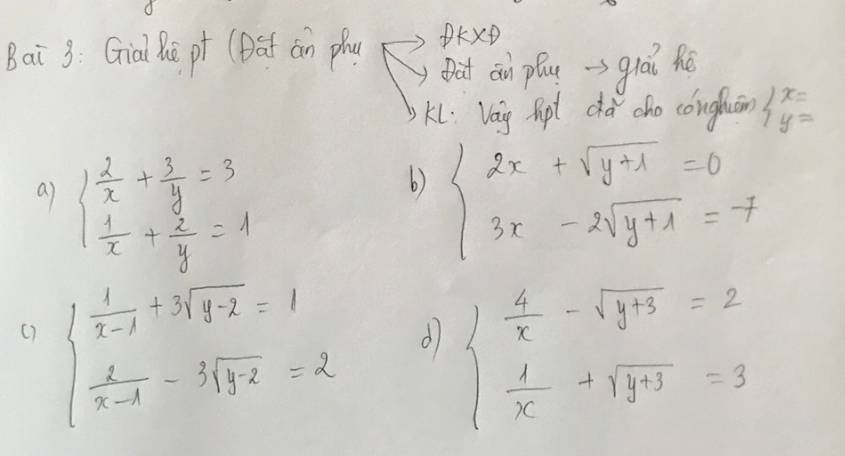Giúp mình với ạ, mình cần gấp trong hôm nay ạ 🙏
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HK
2
23 tháng 4 2022
1)sao phân biệt được v của ai A hay B sửa vA và vB
a)thời gian của hai xe gặp nhau
t=sAB/vA+vB=2/9h=800s
b)sau 0,5h thì người đi từ A đi được
sA=vA.tA=30km
sau 0,5h thì người đi từ B đi được
sB=vB.tB=15km
khoảng cách của hai xe lúc này
s1=(sA+sB)-sAB=25km
c)sau 1h thì người đi từ A đi được
sA1=vA.tA1=60km
sau 1h thì người đi từ B đi được
sB1=vB.tB1=30km
khoảng cách của hai xe lúc này
s2=(sA+sB)-sAB=70km
d)tổng quãng đường đi được ;20-10=10km
sA+sB=10
vA.tA2+vB.tB2=10
60.t+30.t=10
90t=10
t=1/9h
23 tháng 4 2022
câu 2,3 giống cách làm nhưng đáp án khác dựa vào đó làm dễ mà
AH
1
16 tháng 9 2023
b: ĐKXĐ: y>=-1
Đặt \(\left\{{}\begin{matrix}x=a\\\sqrt{y+1}=b\left(b>=0\right)\end{matrix}\right.\)
Hệ phương trình sẽ trở thành:
2a+b=0 và 3a-2b=-7
=>4a+2b=0 và 3a-2b=-7
=>a=-1 và b=2
=>x=-1 và y+1=4
=>x=-1 và y=3
c: ĐKXĐ: x<>1 và y>=2
\(\left\{{}\begin{matrix}\dfrac{1}{x-1}=a\\\sqrt{y-2}=b\left(b>=0\right)\end{matrix}\right.\)
Hệ phương trình sẽ trở thành:
a+3b=1 và 2a-3b=2
=>3a=3 và a+3b=1
=>a=1 và b=0
=>x-1=1 và y-2=0
=>x=2 và y=2
d: ĐKXĐ: x<>0 và y>=-3
Đặt \(\left\{{}\begin{matrix}\dfrac{1}{x}=a\\\sqrt{y+3}=b\left(b>=0\right)\end{matrix}\right.\)
Hệ phương trình sẽ trở thành:
4a-b=2 và a+b=3
=>5a=5 và a+b=3
=>a=1 và b=2
=>x=1 và y+3=4
=>x=1 và y=1
NQ
0
23 tháng 8 2023
\(2^4.5-\left[31-9^2\right]=16.5-\left(31-81\right)=80-\left(-50\right)=130\)
23 tháng 8 2023
\(2^4\).5-[1.31-(13-4)^2]
=16.5-[1.31-81]
=16.5-[31-81]
=16.5-(-50)
=80-(-50)
=130
29 tháng 8 2021
a: Ta có: \(\sqrt{x^2-4x+4}=\sqrt{4x^2-12x+9}\)
\(\Leftrightarrow\left|x-2\right|=\left|2x-3\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=x-2\\2x-3=2-x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{5}{3}\end{matrix}\right.\)
29 tháng 8 2021
c: Ta có: \(\sqrt{4x^2-4x+1}=\sqrt{x^2-6x+9}\)
\(\Leftrightarrow\left|2x-1\right|=\left|x-3\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=x-3\\2x-1=3-x\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=\dfrac{4}{3}\end{matrix}\right.\)