Một đĩa quay đều quanh trục qua tâm O với vận tốc qua tâm là 300 vòng/phút.
Tính tốc độ dài, gia tốc hướng tâm của 1 điểm trên đĩa cách tâm 10cm, g=10m/s2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
8 tháng 9 2017
Chọn đáp án D
+ Theo bài ra ta có f = 300 vòng/ phút = 5 vòng/s
+ Vậy tốc độ góc 
+ Chu kỳ quay: T=1/f=0,2s
+ Vận tốc dài 
+ Gia tốc hướng tâm:
VT
2 tháng 2 2018
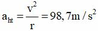
Chọn đáp án C
+ Tốc độ góc: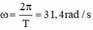 
+ Tốc độ dài: 
+ Gia tốc hướng tâm: 
TK
12 tháng 10 2021
Đổi 30 cm =0,3 m; 1 phút =60s
a,\(T=\dfrac{1}{f}=\dfrac{1}{\dfrac{N}{t}}=\dfrac{1}{\dfrac{60}{60}}=1\left(s\right)\)
\(\omega=\dfrac{2\pi}{T}=2\pi\left(\dfrac{rad}{s}\right)\)
b,\(v=\dfrac{2\pi}{T}\cdot r=0,6\pi\left(\dfrac{m}{s}\right)\)
\(a_{ht}=\dfrac{v^2}{r}=\dfrac{\left(0,6\pi\right)^2}{0,3}=1,2\pi^2\left(\dfrac{m}{s^2}\right)\)
c, Đổi 10 cm =0,1m
Khoảng cách từ tâm đến điểm được xét =0,3-0,1=0,2(m)
<Rùi tính tiếp>
\(v'=\dfrac{2\pi}{T}r'=0,4\pi\left(\dfrac{m}{s}\right)\)
\(a_{ht}'=\dfrac{v'^2}{r'}=\dfrac{\left(0,4\pi\right)^2}{0,3}=\dfrac{8}{15}\pi^2\left(\dfrac{m}{s^2}\right)\)
VT
8 tháng 9 2017
Tốc độ góc của điểm A và điểm B bằng nhau: ω A = ω B
Tốc độ dài của điểm A và điểm B khác nhau:
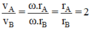
Gia tốc hướng tâm của điểm A và điểm B khác nhau:
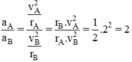
10cm=0,1m
\(\omega=\dfrac{2\pi.300}{60}\)=10\(\pi\)(rad/s)
aht=\(\omega^2.R\)\(\approx\)98,69m/s2