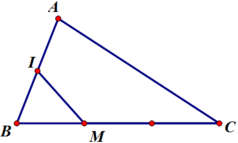
Cho tam giác ABC có M thuộc cạnh BC sao cho CM=2MB và I là trung điểm của AB . Tính IM theo AB và AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 10 2018
CI+ IM= 2MI+ 2IB
3IM= -CI+ 2IB
3IM= -1/2CA-1/2CB+ AB
3IM= 1/2AC+ 1/2 BC+ 1/2AB + 1/2AB
3IM= AC+ 1/2 AB
IM= 1/3AC+ 1/6 AB
CM
14 tháng 8 2017
Chọn C.
Theo định lí hàm cosin, ta có : 
Do MC = 2MB nên BM = 1/3.BC = 2.
Theo định lí hàm cosin, ta có: AM2 = AB2 + BM2 - 2AB.BM.cos B = 42 + 22 -2.4.2.1/2 = 12
Do đó: 
.
26 tháng 2 2023
a: Xét ΔABC có AH/AB=AK/AC
nên HK//BC
b: Xet ΔABC có HK//BC
nên AH/AB=HK/BC
=>HK/18=6/9=2/3
=>HK=12(cm)
c: Xét ΔABM có HI//BM
nên HI/BM=AI/AM
Xét ΔAMC có IK//MC
nên IK/MC=AI/AM
=>HI/BM=IK/MC
mà BM=CM
nên HI=IK
=>I là trung điểm của HK
13 tháng 10 2021
Xét ΔBDC có
M là trung điểm của BC
E là trung điểm của DB
Do đó: ME là đường trung bình của ΔBDC
Suy ra: ME//DC
Xét ΔAME có
D là trung điểm của AE
DI//EM
Do đó: I là trung điểm của AM
hay AI=IM
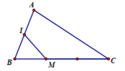
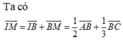
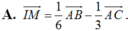
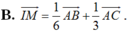
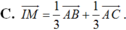
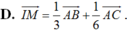
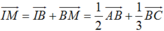
véctơ hay đoạn thẳng CM, MB, IM, AB, AC ?
tính \(\overrightarrow{IM}\) theo \(\overrightarrow{AB}\) và \(\overrightarrow{AC}\)