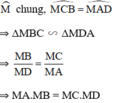Cho điểm A cố định ở bên trong đường tròn (O;R) và A không trùng với O. BC là dây cung quay quanh A. Xác định vị trí của dây cung BC lúc dây BC ngắn nhất.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 7 2023
a: góc AMO+góc ANO=180 độ
=>AMON nội tiếp
b: Xét ΔAKM và ΔAMI có
góc AMK=góc AIM
góc MAK chung
=>ΔAKM đồng dạng với ΔAMI
=>AK/AM=AM/AI
=>AM^2=AI*AK
Xét ΔABM và ΔAMC có
góc AMB=góc ACM
góc BAM chung
=>ΔABM đồng dạng với ΔAMC
=>AB/AM=AM/AC
=>AM^2=AB*AC=AK*AI
16 tháng 6 2023
a: góc SAO=góc SHO=90 độ
=>SAHO nội tiếp
b: Xét ΔSAB và ΔSCA có
góc SAB=góc SCA
góc ASB chung
=>ΔSAB đồng dạng với ΔSCA
=>SA^2=SB*SC
2 tháng 7 2023
a: góc AMO+góc ANO=180 độ
=>AMON nội tiếp
b: ΔOBC cân tại O có OI là trung tuyến
nên OI vuông góc BC
Xét (O) có
AM,AN là tiếp tuyến
=>AM=AN
mà OM=ON
nên OA là trung trực của MN
=>OA vuông góc MN tại H
Xét ΔAHK vuông tại H và ΔAIO vuông tại I có
góc HAK chung
=>ΔAHK đồng dạng vớiΔAIO
=>AH/AI=AK/AO
=>AH*AO=AK*AI=AB*AC
CM
10 tháng 9 2019
Gọi bán kính của đường tròn (O) là R
Ta có:MB=MA+AB = MA + 2R
Suy ra: MA =MB – 2R
Ta lại có: M T 2 = MA.MB (cmt)
Suy ra: M T 2 = (MB- 2R).MB = M B 2 – 2R.MB
CM
8 tháng 1 2017
TH1: M nằm trong đường tròn.
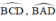là hai góc nội tiếp cùng chắn cung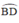 
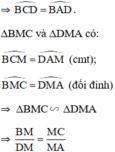
⇒ MA.MB = MC.MD
TH2: M nằm ngoài đường tròn.
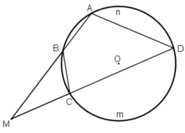
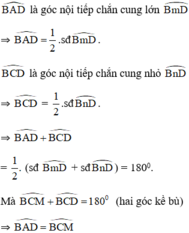
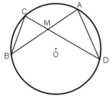
ΔMBC và ΔMDA có:
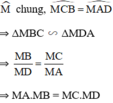
Kiến thức áp dụng
+ Góc nội tiếp chắn một cung có số đo bằng một nửa số đo của cung đó.
+ Hai góc nội tiếp chắn cùng một cung thì có số đo bằng nhau.
CM
18 tháng 7 2018
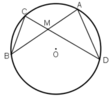
TH1: M nằm trong đường tròn.
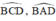là hai góc nội tiếp cùng chắn cung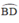 
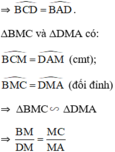
⇒ MA.MB = MC.MD
TH2: M nằm ngoài đường tròn.
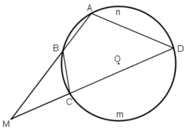
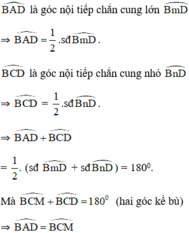
ΔMBC và ΔMDA có:
