Cho ba điểm A(-1;1) ,B(1;3), C(-2;0)
a. Chứng minh ba điểm A,B,C thẳng hàng
b. Tìm các tỉ số mà điểm A chia d0oạn BC, điểm B chia d0oạn AC, điểm C chia đoạn AB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
28 tháng 9 2023
a) Ta có: \(\overrightarrow {AB} = \left( {2;4} \right),\overrightarrow {AG} = \left( {2;1} \right)\)
Do \(\overrightarrow {AB} \ne k.\overrightarrow {AG} \) nên A, B, G không thẳng hàng
b) Giả sử C có tọa độ là: \(C\left( {{x_C};{y_C}} \right)\)
Để G là trọng tâm tam giác ABC thì: \(\left\{ \begin{array}{l}{x_G} = \frac{{{x_A} + {x_B} + {x_C}}}{3}\\{y_G} = \frac{{{y_A} + {y_B} + {y_C}}}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_C} = 3{x_G} - {x_A} - {x_B}\\{y_C} = 3{y_G} - {y_A} - {y_B}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_C} = 3.1 - \left( { - 1} \right) - 1 = 3\\{y_C} = 3.2 - 1 - 5 = 0\end{array} \right.\)
Vậy tọa độ điểm C là: \(C\left( {3;0} \right)\)
CM
18 tháng 11 2019
Chọn A
Điểm N(x;y;0). Tìm x;y từ hệ hai phương trình NA = NB = NC.
NN
1
30 tháng 12 2022
\(\overrightarrow{AB}=\left(-4;-12\right)\)
\(\overrightarrow{AC}=\left(-1;-6\right)\)
Vì -4/-1<>-12/-6
nên A,B,C ko thẳng hàng
CM
16 tháng 8 2019
Gọi (Q) và (R) theo thứ tự là mặt phẳng trung trực của AB và BC.
Những điểm cách đều ba điểm A, B, C là giao tuyến ∆ = (Q) ∩ (R).
(Q) đi qua trung điểm E(3/2; 1/2; 1) của AB và có n Q → = AB→ (1; -3; 0) do đó phương trình của (Q) là: x - 3/2 - 3(y - 1/2) = 0 hay x - 3y = 0
(R) đi qua trung điểm F(1; 1; 1) của BC và có n R → = BC → = (-2; 4; 0) do đó phương trình (R) là: x - 2y + 1 = 0
Ta có: n Q → ∧ n R → = (0; 0; -2).
Lấy D(-3; -1; 0) thuộc (Q) ∩ (R)
Suy ra ∆ là đường thẳng đi qua D và có vectơ chỉ phương u → (0; 0; 1)
nên có phương trình là: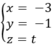 
AH
Akai Haruma
Giáo viên
15 tháng 9 2021
Lời giải:
a. Gọi ptdt $(d)$ đi qua $A,B$ là $y=ax+b$
Ta có: \(\left\{\begin{matrix} y_A=ax_A+b\\ y_B=ax_B+b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 2=a+b\\ 1=a.0+b\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} b=1\\ a=1\end{matrix}\right.\)
Vậy ptđt $(d)$ là: $y=x+1$
b. Ta thấy: $y_C=-4=-5+1=x_C+1$ nên $C\in (d): y=x+1$
Tức là $C$ thuộc đt đi qua 2 điểm $A,B$
$\Rightarrow A,B,C$ thẳng hàng.
HQ
Hà Quang Minh
Giáo viên
28 tháng 9 2023
a) Ta có: \(\overrightarrow {AB} = \left( {3;2} \right),\overrightarrow {AC} = \left( { - 1; - 3} \right)\)
Do \(\overrightarrow {AB} \ne k.\overrightarrow {AC} \) nên A, B, C không thẳng hàng
b) Giả sử tọa độ điểm D là:\(D\left( {{x_D},{y_D}} \right)\)
Ta có: \(\overrightarrow {CD} = \left( {{x_D} - 0;{y_D} - \left( { - 2} \right)} \right) = \left( {{x_D};{y_D} + 2} \right)\)
Để tứ giác ABCD là hình thang có AB // CD và CD= 2AB thì \(\overrightarrow {CD} = 2\overrightarrow {AB} \)
Vậy nên \(\overrightarrow {CD} = 2\overrightarrow {AB} \Leftrightarrow \left\{ \begin{array}{l}{x_D} = 2.3\\{y_D} + 2 = 2.2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_D} = 6\\{y_D} = 2\end{array} \right.\)
Vậy tọa độ D là: \(D\left( {6;2} \right)\)
PT
1
CM
23 tháng 10 2017
Ta có: AB → = (−1; −2; 1)
AC → = (−1; −3; 0)
Ba điểm A, B, C thẳng hàng khi và chỉ khi hai vecto AB → và AC → cùng phương, nghĩa là AB → = k AC → với k là một số thực.
Giả sử ta có AB → = k AC →
khi đó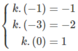 
Ta không tìm được số k nào thỏa mãn đồng thời cả ba đẳng thức trên. Vậy ba điểm A, B, C không thẳng hàng.
11 tháng 12 2021
\(\overrightarrow{AB}=\left(-3;6\right)\)
\(\overrightarrow{AC}=\left(-3,5;7\right)\)
Vì \(\overrightarrow{AB}=\dfrac{7}{6}\overrightarrow{AC}\)
nên A,B,C thẳng hàng
25 tháng 10 2015
vì khi a,b,c thẳng hàng mà b,c,d cũng thẳng hàng.Nên a,b,c,d thẳng hàng
tích đúng nha
a: \(\overrightarrow{AB}=\left(2;2\right)\)
\(\overrightarrow{AC}=\left(-1;-1\right)\)
Vì 2/-1=2/-1
nên A,B,C thẳng hàng
b: \(AB=\sqrt{2^2+2^2}=2\sqrt{2}\)
\(AC=\sqrt{\left(-1\right)^2+\left(-1\right)^2}=\sqrt{2}\)
\(BC=\sqrt{\left(-2-1\right)^2+\left(0-3\right)^2}=3\sqrt{2}\)
=>AB/BC=2/3; AC/BC=1/3; AB/AC=2