tìm các số hữu tỉ thỏa mãn \(x+\sqrt{5}z=\sqrt{7}y\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DD
1
14 tháng 9 2016
Chia làm hai trường hợp :
TH1. Nếu x = y = z = 0 thì thỏa mãn đề bài.
TH2. Nếu \(x,y,z\ne0\) thì ta có : \(x=\sqrt{7}y-\sqrt{5}x\) .
Dễ dàng chứng minh được \(\sqrt{5}\) và \(\sqrt{7}\) là các số vô tỉ . Mặt khác vì \(x,y,z\ne0\) nên \(\sqrt{7}y-\sqrt{5}x\) là số vô tỉ (Vô lí vì x là số hữu tỉ)
Vậy trường hợp này không xảy ra.
Vậy x = y = z = 0
DT
24 tháng 5 2019
Ta có \(\frac{x-y\sqrt{2019}}{y-z\sqrt{2019}}=\frac{m}{n}\left(m,n\varepsilonℤ,\left(m,n\right)=1\right).\)
\(\Rightarrow nx-ny\sqrt{2019}=my-mz\sqrt{2019}\Leftrightarrow nx-my=\sqrt{2019}\left(ny-mz\right).\)\(\Rightarrow\hept{\begin{cases}nx-my=0\\ny-mz=0\end{cases}\Rightarrow}\frac{x}{y}=\frac{y}{z}=\frac{m}{n}\Rightarrow xz=y^2.\)
Khi đó \(x^2+y^2+z^2=\left(x+z\right)^2-2xz+y^2=\left(x+z\right)^2-2y^2+y^2=\left(x+z\right)^2-y^2\)
\(=\left(x-y+z\right)\left(x+y+z\right)\)
Vì \(x+y+z\)là số nguyên lớn hơn 1 và \(x^2+y^2+z^2\)là số nguyên tố nên
\(\hept{\begin{cases}x^2+y^2+z^2=x+y+z\\x-y+z=1\end{cases}\Leftrightarrow}x=y=z=1\)(chỗ này bn tự giải chi tiết nhé, và thử lại nữa)
Kết luận...
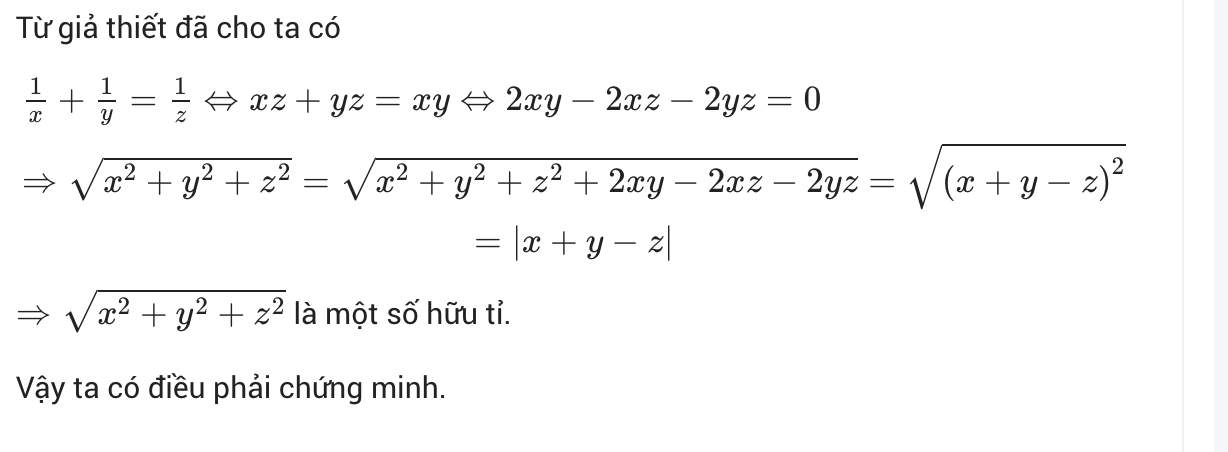
Bình phương 2 vế ta được:
\(\Rightarrow x^2+5z^2+2\sqrt{5}xz=7y^2.\)
\(\Rightarrow\frac{7y^2-x^2-5z^2}{2xz}=\sqrt{5}\)
Vì x;y;z hữu tỉ nên VT hữu tỉ
mà VP vô tỉ
Vậy không tồn tại x;y;z hữu tỉ thoả mãn điều kiện trên