Cho tam giác ABC, O là điểm bất kỳ nằm trong tam giác, góc A=90o. Kẻ OD\(\perp\)BC, OE\(\perp\)CA, OF\(\perp\)AB. Chứng minh rằng OD2+OE2+OF2 \(\ge\)\(\dfrac{AH^2}{2}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TP
28 tháng 8 2017
Giải
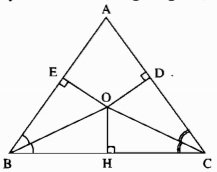
Kẻ OH⊥BC
Xét hai tam giác vuông OEB và OHB, ta có:
\(\widehat{\text{OEB}}=\widehat{\text{OHB}}\)=90o
Cạnh huyền OB chung
\(\widehat{EBO}=\widehat{\text{HB}O}\)(gt)
Suy ra: ∆OEB = ∆OHB (cạnh huyền, góc nhọn)
⇒ OE = OH (hai cạnh tương ứng) (1)
Xét hai tam giác vuông OHC và ODC, ta có:
\(\widehat{\text{OHC}}=\widehat{\text{ODC}}\)=90oCạnh huyền OC chung
\(\widehat{\text{HCO}}=\widehat{\text{DCO}}\)(gt)
Suy ra: ∆OHC = ∆ODC (cạnh huyền, góc nhọn)
⇒ OH = OD (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra: OE = OD.
17 tháng 7 2019
Vì ∆ABC đều
=> A = B = C
Vì OD // BC ( gt)
=> ODEB là hình thang
Vì OE//AC(gt)
=> C = DEB ( đồng vị)
Mà B = C
=> B = DEB
=> DOEB là hình thang cân
Vì OE // AC
=> EOFC là hình thang
Vì OF//AB
=> A = BFC ( đồng vị)
Mà A = C (cmt)
=> C = BFC
=> EOFC là hình thang cân
Vì OF // AB
=> FODA là hình thang
Mà OD //BC
=> ADF = B
Mà A = B
=> A = ADF
=> FODA là hình thang cân
Vì DOEB là hình thang cân
Mà B = OEB = 60°
=> BDO = DOE = 120°
Chứng minh tương tự ta có
DOE = DOF = FOD = 120°
17 tháng 7 2019
Trong hình thang cân hai đường chéo bằng nhai
=> OA = DF
=> OB = DE
=> OC = EF
Vì 3 đoạn thẳng OA ; OB ; OC lần lượt là bằng 3 cạnh của ∆DEF
=> 3 đoạn thẳng OA ; OB ; OC thỏa mãn bất đẳng thức tam giác
28 tháng 7 2023
Ta có: Xét tứ giác AEHF có:
+\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^o\)
=>AEHF là hình chữ nhật (dhnb)
=>AH cắt ED tại trung điểm mỗi đường (dhnb)
Mà AH=EF
\(\Rightarrow OE=OF=\dfrac{AH}{2}\\ \Rightarrow HB.HC=AH^2\\ \Rightarrow4.OE.OF=AH.FE.AH^2\)
Vậy HB.HC=4.OE.OF
30 tháng 3 2022
a: Xét ΔCIA vuông tại I và ΔCIB vuông tại I có
CA=CB
CI chung
Do đó: ΔCIA=ΔCIB
Suy ra: IA=IB
b: Xét ΔCHI vuông tại H và ΔCKI vuông tại K có
CI chung
\(\widehat{HCI}=\widehat{KCI}\)
Do đó: ΔCHI=ΔCKI
Suy ra: IH=IK
c: IA=IB=AB/2=6(cm)
nen IC=8(cm)
d: Xét ΔCAB có CH/CA=CK/CB
nên HK//AB