42x-1 :4 = 12
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NQ
0
PT
1
CM
16 tháng 8 2019
Tập xác định: D = R.
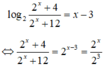
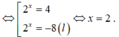
Vậy phương trình đã cho có nghiệm duy nhất
Chọn B
AH
Akai Haruma
Giáo viên
6 tháng 1
Lời giải:
a. $(x^2-9)(5x+15)=0$
$\Rightarrow x^2-9=0$ hoặc $5x+15=0$
Nếu $x^2-9=0$
$\Rightarrow x^2=9=3^2=(-3)^2$
$\Rightarrow x=3$ hoặc $-3$
Nếu $5x+15=0$
$\Rightarrow x=-3$
b.
$x^2-8x=0$
$\Rightarrow x(x-8)=0$
$\Rightarrow x=0$ hoặc $x-8=0$
$\Rightarrow x=0$ hoặc $x=8$
c.
$5+12(x-1)^2=53$
$12(x-1)^2=53-5=48$
$(x-1)^2=48:12=4=2^2=(-2)^2$
$\Rightarrow x-1=2$ hoặc $x-2=-2$
$\Rightarrow x=3$ hoặc $x=0$
d.
$(x-5)^2=36=6^2=(-6)^2$
$\Rightarrow x-5=6$ hoặc $x-5=-6$
$\Rightarrow x=11$ hoặc $x=-1$
e.
$(3x-5)^3=64=4^3$
$\Rightarrow 3x-5=4$
$\Rightarrow 3x=9$
$\Rightarrow x=3$
f.
$4^{2x}+2^{4x+3}=144$
$2^{4x}+2^{4x}.8=144$
$2^{4x}(1+8)=144$
$2^{4x}.9=144$
$2^{4x}=144:9=16=2^4$
$\Rightarrow 4x=4\Rightarrow x=1$
HQ
Hà Quang Minh
Giáo viên
11 tháng 8 2023
\(4^{2x-1}:4=4^4\\ \Leftrightarrow4^{2x-2}=4^4\\ \Leftrightarrow2x-2=4\\ \Leftrightarrow2x=6\\ \Leftrightarrow x=3\)
15 tháng 9 2021
\(\Leftrightarrow30x^2-72x+55x-132-42x+66=0\\ \Leftrightarrow30x^2-59x-66=0\\ \Delta=3481-4\cdot\left(-66\right)\cdot30=11401\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{59-\sqrt{11401}}{60}\\x=\dfrac{59+\sqrt{11401}}{60}\end{matrix}\right.\)
26 tháng 12 2020
4^2x+1+4^2x=20
4^2x.4^1+4^2x.1=20
4^2x.(4^1+1)=20
4^2x.5=20
4^2x=20:5
4^2x=4
4^2x=2^2
2x=2
x=2:2
x=1
sai đừng trách mk còn đúng thì 1 like
LD
26 tháng 12 2020
4^2x+1+4^2x=20
4^2x.4^1+4^2x.1=20
4^2x.(4^1+1)=20
4^2x.5=20
4^2x=20:5
4^2x=4
4^2x=2^2
2x=2
27 tháng 5 2022
Câu 1:
\(\sqrt{x^2-2x+1}+\sqrt{x^2-4x+4}=3\)
\(\Leftrightarrow\left|x-1\right|+\left|x-2\right|=3\)(1)
Trường hợp 1: x<1
(1) trở thành 1-x+2-x=3
=>3-2x=3
=>x=0(nhận)
Trường hợp 2: 1<=x<2
(1) trở thành x-1+2-x=3
=>1=3(loại)
Trường hợp 3: x>=2
(1) trở thành x-1+x-2=3
=>2x-3=3
=>2x=6
hay x=3(nhận)
TD
1
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 9 2020
Do \(-1\le sin2x;cos2x\le1\Rightarrow\left\{{}\begin{matrix}sin^42x\le sin^22x\\cos^42x\le cos^22x\end{matrix}\right.\)
\(\Rightarrow sin^42x+cos^42x\le sin^22x+cos^22x=1\)
Dấu "=" xảy ra khi và chỉ khi:
\(\left[{}\begin{matrix}sin2x=0\\cos2x=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=\frac{k\pi}{2}\\x=\frac{\pi}{4}+\frac{k\pi}{2}\end{matrix}\right.\)
co sai de ko do thay sai sai sao ay