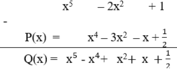Cho các đa thức P(x), Q(x), R(x), S(x) thỏa mãn
P ( x5) + xQ (x10) + x2R( x15 ) + ( x4 - x3 + x2 - x + 1)S(x), \(\forall x\inℝ\)
.
Chứng minh rằng x +1 là ước Q(x) .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì P(x) có hệ số bậc cao nhất là 1
Nên P(x) có thể được viết dưới dạng: \(P\left(x\right)=\left(x-x_1\right)\left(x-x_2\right)\left(x-x_3\right)\left(x-x_4\right)\left(x-x_5\right)\)
Và \(P\left(-1\right)=\left(-1\right)^5-5\left(-1\right)^3+4\left(-1\right)+1=1\)
\(P\left(\frac{1}{2}\right)=\frac{77}{32}\)
Ta có: \(Q\left(x\right)=2x^2+x-1=2x^2+2x-x-1=2x\left(x+1\right)-\left(x+1\right)=\left(x+1\right)\left(2x-1\right)\)
=> \(Q\left(x_1\right).\text{}\text{}Q\left(x_2\right).\text{}\text{}Q\left(x_3\right).\text{}\text{}Q\left(x_4\right).\text{}\text{}Q\left(x_5\right)\text{}\text{}\)
\(=\left(x_1+1\right)\left(2x_1-1\right)\left(x_2+1\right)\left(2x_2-1\right)\left(x_3+1\right)\left(2x_3-1\right)\left(x_4+1\right)\left(2x_4-1\right)\left(x_5+1\right)\left(2x_5-1\right)\)
\(=32\left(-1-x_1\right)\left(\frac{1}{2}-x_1\right)\left(-1-x_2\right)\left(\frac{1}{2}-x_2\right)\left(-1-x_3\right)\left(\frac{1}{2}-x_3\right)\left(-1-x_4\right)\left(\frac{1}{2}-x_4\right)\left(-1-x_5\right)\left(\frac{1}{2}-x_5\right)\)\(=32.P\left(-1\right).P\left(\frac{1}{2}\right)=32.1.\frac{77}{32}=77\)
\(p\left(x\right)=x^5-5x^3+4x+1=\left(x-x_1\right)\left(x-x_2\right)\left(x-x_3\right)\left(x-x_4\right)\left(x-x_5\right)\)
\(Q\left(x\right)=2\left(\frac{1}{2}-x\right)\left(-1-x\right)\)
Do đó \(Q\left(x_1\right)\cdot Q\left(x_2\right)\cdot Q\left(x_3\right)\cdot Q\left(x_4\right)\cdot Q\left(x_5\right)\)
\(=2^5\left[\left(\frac{1}{2}-x_1\right)\left(\frac{1}{2}-x_2\right)\left(\frac{1}{2}-x_3\right)\left(\frac{1}{2}-x_4\right)\left(\frac{1}{2}-x_5\right)\right]\)
\(=\left(-1-x_1\right)\left(-1-x_2\right)\left(-1-x_3\right)\left(-1-x_4\right)\left(-1-x_5\right)\)
\(=32P\left(\frac{1}{2}\right)\cdot\left[P\left(-1\right)\right]\)
\(=32\cdot\left(\frac{1}{32}-\frac{5}{8}+\frac{4}{2}+1\right)\left(-1+5-4+1\right)\)
\(=4300\)
*Mình không chắc*

a.\(P\left(x\right)=1+3x^5-4x^2+x^5+x^3-x^2+3x^3\)
\(=1-5x^2+4x^3+4x^5\)
\(Q\left(x\right)=2x^5-x^2+4x^5-x^4+4x^2-5x\)
\(=-5x+3x^2+3x^4+2x^5\)
b.\(P\left(x\right)+Q\left(x\right)=1-5x^2+4x^3+4x^5-5x+3x^2+3x^4+2x^5\)
\(=6x^5+3x^4+4x^3-2x^2-5x+1\)
\(P\left(x\right)-Q\left(x\right)=1-5x^2+4x^3+4x^5+5x-3x^2-3x^4-2x^5\)
\(=2x^5-3x^4+4x^3-8x^2+5x+1\)
c.\(P\left(x\right)+Q\left(x\right)=6x^5+3x^4+4x^3-2x^2-5x+1\)
\(x=-1\)
\(P\left(x\right)+Q\left(x\right)=6.\left(-1\right)^5+3.\left(-1\right)^4+4.\left(-1\right)^3-5.\left(-1\right)+1\)
\(=-6+3-4+5+1=-1\)
d.\(Q\left(0\right)=\)\(-5x+3x^2+3x^4+2x^5\)
\(=0\)
\(P\left(0\right)=\)\(1-5x^2+4x^3+4x^5\)
\(=1\)
Vậy x=0 ko là nghiệm của đa thức P(x)

\(P\left(x\right)=x^5-2+x+x^3+x^2=x^5+x^3+x^2+x-2\)
\(Q\left(x\right)=-x+4x^5+x^4+x^2+x^3=4x^5+x^4+x^3+x^2-x\)
\(P\left(x\right)+Q\left(x\right)=\left(x^5+4x^5\right)+x^4+\left(x^3+x^3\right)+\left(x^2+x^2\right)+\left(x-x\right)-2\)
\(P\left(x\right)+Q\left(x\right)=5x^5+x^4+2x^3+2x^2-2\)
\(P\left(x\right)-Q\left(x\right)=\left(x^5-4x^5\right)-x^4+\left(x^3-x^3\right)+\left(x^2-x^2\right)+\left(x+x\right)-2\)
\(P\left(x\right)-Q\left(x\right)=-3x^5-x^4+2x-2\)

`@` `\text {Ans}`
`\downarrow`
`a)`
Thu gọn:
`P(x)=`\(5x^4 + 3x^2 - 3x^5 + 2x - x^2 - 4 +2x^5\)
`= (-3x^5 + 2x^5) + 5x^4 + (3x^2 - x^2) + 2x - 4`
`= -x^5 + 5x^4 + 2x^2 + 2x - 4`
`Q(x) =`\(x^5 - 4x^4 + 7x - 2 + x^2 - x^3 + 3x^4 - 2x^2\)
`= x^5 + (-4x^4 + 3x^4) - x^3 + (x^2 - 2x^2) + 7x - 2`
`= x^5 - x^4 - x^3 - x^2 + 7x - 2`
`@` Tổng:
`P(x)+Q(x)=`\((-x^5 + 5x^4 + 2x^2 + 2x - 4) + (x^5 - x^4 - x^3 - x^2 + 7x - 2)\)
`= -x^5 + 5x^4 + 2x^2 + 2x - 4 + x^5 - x^4 - x^3 - x^2 + 7x - 2`
`= (-x^5 + x^5) - x^3 + (5x^4 - x^4) + (2x^2 - x^2) + (2x + 7x) + (-4-2)`
`= 4x^4 - x^3 + x^2 + 9x - 6`
`@` Hiệu:
`P(x) - Q(x) =`\((-x^5 + 5x^4 + 2x^2 + 2x - 4) - (x^5 - x^4 - x^3 - x^2 + 7x - 2)\)
`= -x^5 + 5x^4 + 2x^2 + 2x - 4 - x^5 + x^4 + x^3 + x^2 - 7x + 2`
`= (-x^5 - x^5) + (5x^4 + x^4) + x^3 + (2x^2 + x^2) + (2x - 7x) + (-4+2)`
`= -2x^5 + 6x^4 + x^3 + 3x^2 - 5x - 2`
`b)`
`@` Thu gọn:
\(H (x) = ( 3x^5 - 2x^3 + 8x + 9) - ( 3x^5 - x^4 + 1 - x^2 + 7x)\)
`= 3x^5 - 2x^3 + 8x + 9 - 3x^5 + x^4 - 1 + x^2 - 7x`
`= (3x^5 - 3x^5) + x^4 - 2x^3 - x^2 + (8x + 7x) + (9+1)`
`= x^4 - 2x^3 - x^2 + 15x + 10`
\(R( x) = x^4 + 7x^3 - 4 - 4x ( x^2 + 1) + 6x\)
`= x^4 + 7x^3 - 4 - 4x^3 - 4x + 6x`
`= x^4 + (7x^3 - 4x^3) + (-4x + 6x) - 4`
`= x^4 + 3x^3 + 2x - 4`
`@` Tổng:
`H(x)+R(x)=` \((x^4 - 2x^3 - x^2 + 15x + 10)+(x^4 + 3x^3 + 2x - 4)\)
`= x^4 - 2x^3 - x^2 + 15x + 10+x^4 + 3x^3 + 2x - 4`
`= (x^4 + x^4) + (-2x^3 + 3x^3) - x^2 + (15x + 2x) + (10-4)`
`= 2x^4 + x^3 - x^2 + 17x + 6`
`@` Hiệu:
`H(x) - R(x) =`\((x^4 - 2x^3 - x^2 + 15x + 10)-(x^4 + 3x^3 + 2x - 4)\)
`=x^4 - 2x^3 - x^2 + 15x + 10-x^4 - 3x^3 - 2x + 4`
`= (x^4 - x^4) + (-2x^3 - 3x^3) - x^2 + (15x - 2x) + (10+4)`
`= -5x^3 - x^2 + 13x + 14`
`@` `\text {# Kaizuu lv u.}`

Ta có:
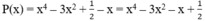
Vì : P(x) + Q(x) = x5 – 2x2 + 1
Suy ra Q(x) = x5 – 2x2 + 1– P(x).