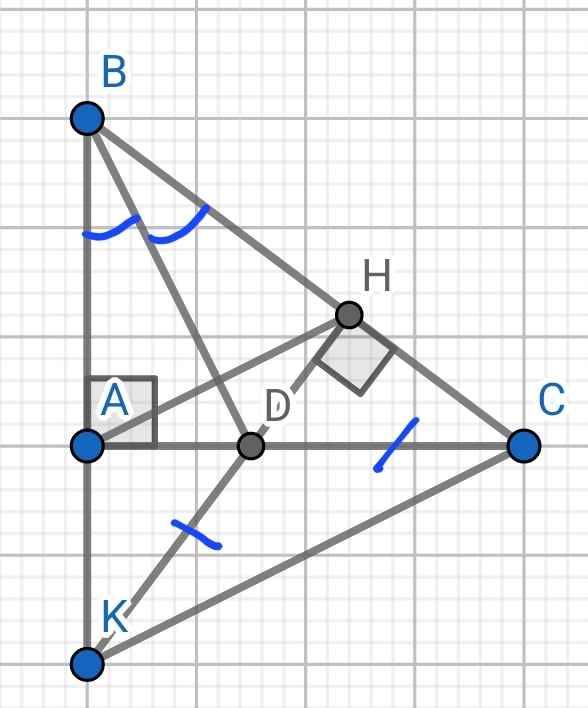
Cho tam giác ABC, D là trung điểm của BC . Trên tia đối của tia DA lấy điểm E sao cho DA=DE
a, Chứng tỏ \(\Delta ADB=\Delta EDC,\widehat{BAE=}\widehat{CEA}\)
B, Vẽ DH vuông góc với ABở H. Chứng tỏ \(HD\perp CE\)
c, Trên tia đối của tia DH , lấy điểm K sao cho DH=DK . Chứng tỏ ba điểmm C,E,K thẳng hàng