Hai tàu thủy A và B ở trên cùng 1 kinh tuyến. Tàu A ở phía bắc của B và cách B 1 khoảng d0.
Tàu A chuyển động đều về phía đông với vận tốc vA, tàu B chuyển động đều lên phía bắc với vận tốc vB. Độ cong của mặt biển k đáng kể.
a/ định khoảng cách cực tiểu giữa tàu A và tàu B?
b/ Tàu B phải chạy theo hướng nào để bắt kịp tàu A. Định thời gian rượt đuổi. Các tàu chuyển động theo quỹ đạo thẳng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

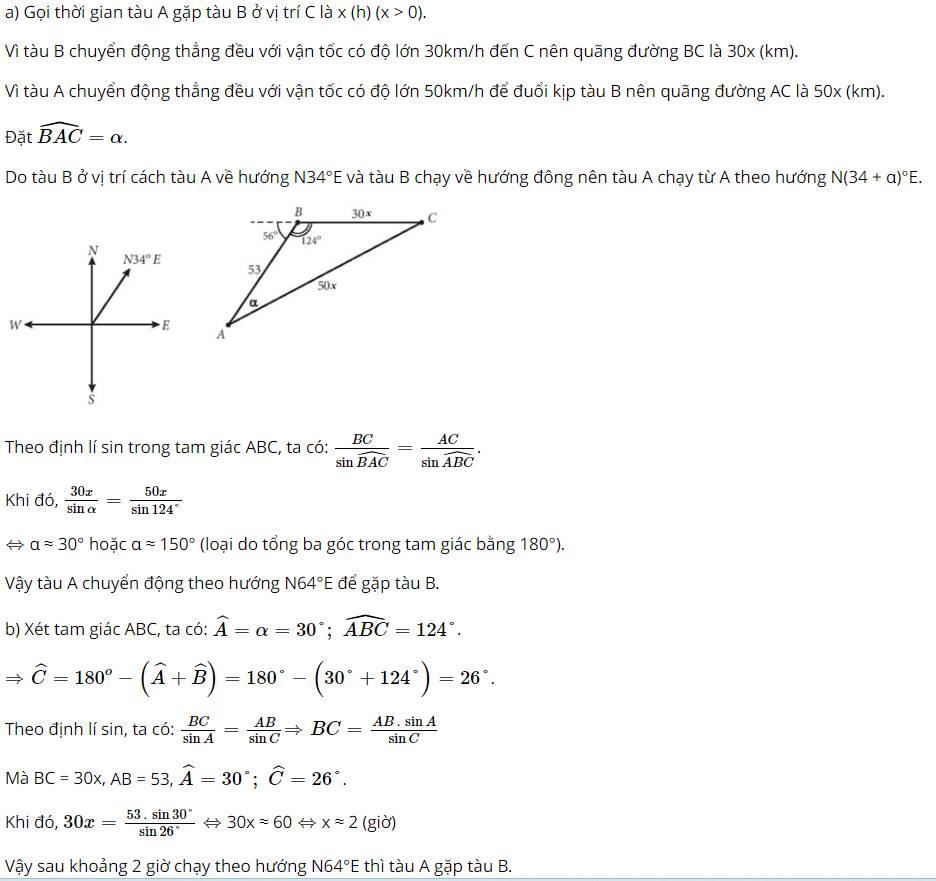
a)
Gọi t (đơn vị: giờ) là thời gian đi cho đến khi hai tàu gặp nhau tại C.
Tàu B đi với vận tốc có độ lớn 30km/h nên quãng đường BC = 30t
Tàu A đi với vận tốc có độ lớn 50km/h nên quãng đường AC = 50t
Theo định lí sin, ta có: \(\frac{a}{{\sin \alpha }} = \frac{b}{{\sin B}}\)
Trong đó: \(\left\{ \begin{array}{l}a = BC = 30t\\b = AC = 50t\\\widehat B = {124^o}\end{array} \right.\)
\(\begin{array}{l} \Rightarrow \frac{{30t}}{{\sin \alpha }} = \frac{{50t}}{{\sin {{124}^o}}}\\ \Leftrightarrow \sin \alpha = \frac{{30t.\sin {{124}^o}}}{{50t}} = \frac{{30.\sin {{124}^o}}}{{50}} \approx 0,4974\end{array}\)
\( \Leftrightarrow \alpha \approx {30^o}\) hoặc \(\alpha \approx {150^o}\)(loại)
Vậy tàu A chuyển động theo hướng tạo với vị trí ban đầu của tàu B góc \({30^o}\).
b) Xét tam giác ABC, ta có:
\(\begin{array}{l}\widehat B = {124^o};\widehat A = {30^o}\\ \Rightarrow \widehat C = {180^o} - \left( {\widehat B + \widehat A} \right) = {180^o} - \left( {{{124}^o} + {{30}^o}} \right) = {26^o}\end{array}\)
Theo định lí sin, ta có
\(\frac{a}{{\sin A}} = \frac{c}{{\sin C}} \Rightarrow a = \frac{{c.\sin A}}{{\sin C}}\)
Mà \(\left\{ \begin{array}{l}a = BC = 30t\\c = AB = 53\\\widehat A = {30^o};\widehat C = {26^o}\end{array} \right. \Rightarrow 30t = \frac{{53.\sin {{30}^o}}}{{\sin {{26}^o}}}\)
\(\begin{array}{l} \Leftrightarrow 30t \approx 60,45\\ \Leftrightarrow t \approx 2\;(h)\end{array}\)
Vậy sau khoảng 2 giờ thì tàu A đuổi kịp tàu B.

Chọn B.
Vì vận tốc của người soát vé so với mặt đất (vng/đ) bằng tổng vận tốc của người so với tàu (vng/tàu) và vận tốc của tàu so với đất (vtàu/đ) nên ta có: vng/đ = vng/tàu + vtàu/đ = 3 + 36 = 39 km/h.

Đáp án C
Sau khi hãm tốc :
Quãng đường tàu thứ nhất đã đi được đến khi dừng là
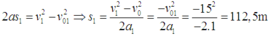
Quãng đường tàu thứ hai đã đi được đến khi dừng là
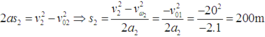
Suy ra, khoảng cách giữa hai tàu là 500 – 112,5 – 200 = 187,5m

Đáp án C
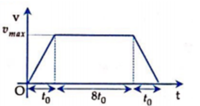
Vẽ đồ thị v – t như hình trên: Khi đó quãng đường vật đi được chính bằng diện tích của hình thang
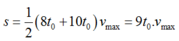
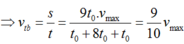

v 1 = 504 k m / h = 140 m / s , v 2 = 90 k m / h = 25 m / s
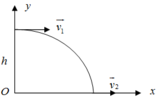
Bom là vật ném theo phương ngang ở độ cao h. Áp dụng phương pháp tọa độ với hệ trục Oxy như hình vẽ.
a. Máy bay và tàu chuyển động cùng chiều:
Đối với máy bay x 1 = v 1 t y 1 = − 1 2 g t 2 + h
Đối với tàu chiến x 2 = v 2 t + s y 2 = 0
Để bom thả trúng tàu thì: x 2 = x 1 ; y 2 = y 1
⇒ − 1 2 g t 2 + h = 0 v 1 t = v 2 t + s ⇒ t = 2 h g ⇒ s = v 1 − v 2 t
Vậy máy bay cách tàu chiến một quãng đường là:
s = v 1 − v 2 2 h g = 140 − 25 . 2.2000 10 = 2300 m = 2 , 3 k m
b. Máy bay và tàu chuyển động ngược chiều.
Chứng minh tương tự câu a ta có
⇒ s = v 1 + v 2 2 h g = 140 + 25 . 2.2000 10 = 3300 m = 3 , 3 k m