cho 4 điểm A(-1;1), B(3;2), C(2-1), D(-2;-2)
a, Lập phương trình đoạn thẳng AB, BC, CD, DA
b, Chứng minh rằng ABCD là hình bình hành
c, Tính diện tích tứ giác ABCD
LÀM CÂU C GIÚP MK VỚI
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ Gọi \(D\left(a;0\right)\) \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-9;3\right)\\\overrightarrow{AD}=\left(a-6;-3\right)\end{matrix}\right.\)
Do A; B; D thẳng hàng \(\Leftrightarrow\frac{a-6}{-9}=\frac{-3}{3}\Rightarrow a=15\) \(\Rightarrow D\left(15;0\right)\)
b/ \(\overrightarrow{AB}=\left(-1;5\right);\) \(\overrightarrow{AD}=\left(-2;10\right)\)
\(\Rightarrow\overrightarrow{AD}=2\overrightarrow{AB}\Rightarrow A,B,D\) thẳng hàng

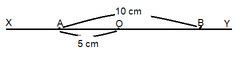
a. điểm O nằm giữa 2 điểm còn lại
b. ta có : OA + OB = AB
hay 5 + OB = 10
OB = 10 - 5 = 5(cm)
c. vì \(OA=OB=\dfrac{AB}{2}=5\left(cm\right)\)
nên O là trung điểm AB

Chọn 1 trong 4 điểm ta vẽ được 3 đường thẳng đi qua 2 điểm
Cứ làm như thế với 4 điểm đó ta vẽ được : 4.3=12 đường thẳng
Vì mỗi đường thẳng được tính 2 lần
=> Số đường thẳng được tạo thành là 12:2=6

Ta có: \(\overrightarrow {AD} \left( { - 2;10} \right),{\mkern 1mu} \overrightarrow {AB} \left( { - 1;5} \right) \Rightarrow \overrightarrow {AD} = 2\overrightarrow {AB} \)
\(\Rightarrow\) 3 điểm \(A,B,D\) thẳng hàng.

Tọa độ trung điểm I của AB là:
\(\left\{{}\begin{matrix}x=\dfrac{1+1}{2}=1\\y=\dfrac{3-1}{2}=\dfrac{2}{2}=1\\z=\dfrac{5+1}{2}=\dfrac{6}{2}=3\end{matrix}\right.\)
vậy: I(1;1;3)

\(\overrightarrow{DA}=\left(1;-1\right)\)
\(\overrightarrow{DC}=\left(4;4\right)=4\left(1;1\right)\)
\(\Rightarrow\overrightarrow{DC}=4\overrightarrow{DA}\) nên 4 điểm D, A, C thẳng hàng