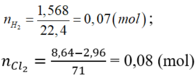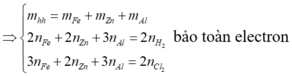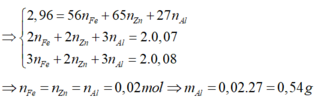Hỗn hợp X gồm Al, Zn và Fe, trong đó khối lượng Al bằng 18/31 tổng khối lượng của Zn và Fe. Hòa tan hết 14,7 gam X bằng lượng dư dd HCl, sau phản ứng thu được 10,08 lít H2(đktc). Xác định % về khối lượng của các kim loại trong hh X?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 3 2022
Trong \(20,4g\) hỗn hợp có: \(\left\{{}\begin{matrix}n_{Zn}=a\left(mol\right)\\n_{Fe}=b\left(mol\right)\\n_{Al}=c\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow65a+56b+27c=20,4\left(1\right)\)
\(n_{H_2}=\dfrac{10,08}{22,4}=0,45mol\)
\(BTe:2n_{Zn}+2n_{Fe}+3n_{Al}=2n_{H_2}\)
\(\Rightarrow2a+2b+3c=2\cdot0,45\left(2\right)\)
Trong \(0,2mol\) hhX có \(\left\{{}\begin{matrix}Zn:ka\left(mol\right)\\Fe:kb\left(mol\right)\\Al:kc\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow ka+kb+kc=0,2\)
\(n_{Cl_2}=\dfrac{6,16}{22,4}=0,275mol\)
\(BTe:2n_{Zn}+3n_{Fe}+3n_{Al}=2n_{Cl_2}\)
\(\Rightarrow2ka+3kb+3kc=2\cdot0,275\)
Xét thương:
\(\dfrac{ka+kb+kc}{2ka+3kb+3kc}=\dfrac{0,2}{2\cdot0,275}\Rightarrow\dfrac{a+b+c}{2a+3b+3c}=\dfrac{4}{11}\)
\(\Rightarrow3a-b-c=0\left(3\right)\)
Từ (1), (2), (3)\(\Rightarrow\left\{{}\begin{matrix}a=0,1mol\\b=0,2mol\\c=0,1mol\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m_{Zn}=6,5g\\m_{Fe}=11,2g\\m_{Al}=2,7g\end{matrix}\right.\)
MN
25 tháng 3 2021
\(n_{Fe}=a\left(mol\right),n_{Mg}=b\left(mol\right),n_{Al}=c\left(mol\right),n_{Zn}=d\left(mol\right)\)
\(n_{H_2}=\dfrac{2.24}{22.4}=0.1\left(mol\right)\)
\(\)\(BTe:\)
\(2a+2b+3c+2d=0.2\left(1\right)\)
\(n_{Cl_2}=\dfrac{3.36}{22.4}=0.15\left(mol\right)\)
\(BTe:\)
\(3a+2b+3c+2c=0.15\cdot2=0.3\left(2\right)\)
\(\left(2\right)-\left(1\right):a=0.3-0.2=0.1\)
\(\%Fe=\dfrac{0.1\cdot56}{32}\cdot100\%=17.5\%\)
Y
14 tháng 12 2020
Gọi a,b lần lượt là số mol của Al, Fe trong hỗn hợp ban đầu
=> 27a+56b=8,3 (1)
\(n_{H_2}=\dfrac{5,6}{22,4}=0,25mol\)
Ta có quá trình trao đổi elcetron
\(Al^0\rightarrow Al^{+3}+3e\)
a----------------3a--(mol)
\(Fe^0\rightarrow Fe^{+2}+2e\)
b----------------2b--(mol)
\(2H^{-1}+2e\rightarrow H_2^0\)
----------0,5------0,25-(mol)
Áp dụng định luật bảo toàn e ta có: 3a+2b=0,5 (2)
Giải hệ phương trình gồm (1) và (2) ta được: \(\left\{{}\begin{matrix}a=0,1\\b=0,1\end{matrix}\right.\)
\(\left[{}\begin{matrix}m_{Al}=0,1\cdot27=2,7g\\m_{Fe}=0,1\cdot56=5,6g\end{matrix}\right.\)
1 tháng 5 2023
Đặt \(\begin{matrix}n_{Al}=a\left(mol\right)\\n_{Fe}=b\left(mol\right)\end{matrix}=>27a+56b=13,8\left(1\right)\)
Pt : \(2Al+6HCl\rightarrow2AlCl_3+3H_2\)
a \(\dfrac{3}{2}\)a
\(Fe+2HCl\rightarrow FeCl_2+H_2\)
b b
\(n_{H2}=\dfrac{10,08}{22,4}=0,45\left(mol\right)=>1,5a+b=0,45\left(2\right)\)
Từ (1),(2) ta có hệ phương trình : \(\left\{{}\begin{matrix}27a+56b=13,8\\1,5a+b=0,45\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=0,2\\b=0,15\end{matrix}\right.\)
\(m_{Al}=0,2.27=5,4\left(g\right)\)
\(m_{Fe}=0,15.56=8,4\left(g\right)\)
Chúc bạn học tốt
1 tháng 5 2023
Ta có: 27nAl + 56nFe = 13,8 (1)
\(n_{H_2}=\dfrac{10,08}{22,4}=0,45\left(mol\right)\)
Theo ĐLBT e, có: 3nAl + 2nFe = 2nH2 = 0,9 (2)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}n_{Al}=0,2\left(mol\right)\\n_{Fe}=0,15\left(mol\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m_{Al}=0,2.27=5,4\left(g\right)\\m_{Fe}=0,15.56=8,4\left(g\right)\end{matrix}\right.\)
