Tìm số hạng tổng quát của các dãy số sau:
a)1;3;6;10;15;...
b)6;14;24;36;50;...
c)4;28;70;130;208;...
d)2;5;9;14;20;...
e)3;6;10;15;21;...
h)2;8;20;40;70;112;...
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Năm số hạng đầu của dãy số là: 3; 9; 19; 33; 51
b) Năm số hạng đầu của dãy số là: \( - 1;\frac{1}{3}; - \frac{1}{5};\frac{1}{7}; - \frac{1}{9}\)
c) Năm số hạng đầu của dãy số là: \(2;2;\frac{8}{3};4;\frac{{32}}{5}\)
d) Năm số hạng đầu của dãy số là: \(2;\frac{9}{4};\frac{{64}}{{27}};\frac{{625}}{{256}};\frac{{7776}}{{3125}}\)
10 tháng 7 2023
a) Ta viết lại dãy đã cho thành \(1\dfrac{1}{3},1\dfrac{1}{8},1\dfrac{1}{15},...\)
Ta có thể thấy mẫu số của phần phân số trong các hỗn số của dãy là dãy các tích của 2 số cách nhau 2 đơn vị kể từ \(1.3\). Chẳng hạn \(3=1.3\), \(8=2.4\), \(15=3.5,...\) Do đó ta rút ra công thức số hạng tổng quát của dãy là \(u_n=1\dfrac{1}{n\left(n+2\right)}\)\(1+\dfrac{1}{n\left(n+2\right)}=\dfrac{n^2+2n+1}{n\left(n+2\right)}=\dfrac{\left(n+1\right)^2}{n\left(n+2\right)}\)
b) Ta cần tính \(u_1.u_2...u_{98}\). Ta thấy rằng
\(u_1.u_2...u_{98}\) \(=\dfrac{\left(1+1\right)^2}{1.3}.\dfrac{\left(2+1\right)^2}{2.4}.\dfrac{\left(3+1\right)^2}{3.5}...\dfrac{\left(98+1\right)^2}{97.99}\) \(=\dfrac{2^2}{1.3}.\dfrac{3^2}{2.4}.\dfrac{4^2}{3.5}.\dfrac{6^2}{4.6}...\dfrac{98^2}{97.99}.\dfrac{99^2}{98.100}\) \(=\dfrac{2.99}{100}=\dfrac{99}{50}\)
DM
0
CM
20 tháng 12 2019
a)Năm số hạng đầu: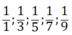 
Số hạng tổng quát của dãy số: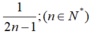 
b)Năm số hạng đầu: 1;4;7;10;13
Số hạng tổng quát của dãy số: 3n + 1(n ∈ N)
LC
3 tháng 9 2015
Ta thấy: 1=(1-1).4+1
5=(2-1).4+1
9=(3-1).4+1
13=(4-1).4+1
17=(5-1).4+1
………………
Quy luật: Mỗi số hạng trong dãy bằng số thứ tự của nó trừ 1 rồi nhân với 4 cuối cùng cộng thêm 1.
a) Gọi số n là số hạng thứ a của dãy.
Ta có: n=(a-1).4+1
=>3 số hạng tiếp theo của dãy là:(6-1).4+1=21
(7-1).4+1=25
(8-1).4+1=29
b)Số hạng thứ 2011 của dãy là: (2011-1).4+1=8041
c)Ta có:S=1+5+9+…+8041
=>\(S=\frac{\left(\left(8041-1\right):4+1\right).\left(8041+1\right)}{2}\)
=>\(S=\frac{\left(8040:4+1\right).8042}{2}\)
=>\(S=\left(2010+1\right).\frac{8042}{2}\)
=>\(S=2011.4021\)
=>\(S=8086231\)
3 tháng 9 2015
a) dạng tổng quát là: 4k + 1
3 số điền vào la 21;25;29
Số thứ 2011 : 4 x 2011 - 4 + 1 = 8041
CM
8 tháng 2 2019
Ta có:
0 = 0 0 + 1 ; 1 2 = 1 1 + 1 ; 2 3 = 2 2 + 1 3 4 = 3 3 + 1 ; 4 5 = 4 4 + 1
Suy ra u n = n n + 1
Chọn đáp án B
10 tháng 12 2022
u1 (n=0) = \(\dfrac{0}{0+1}\)=0
u2 (n=1) = \(\dfrac{1}{1+1}\)=\(\dfrac{1}{2}\)
u3 (n = 2) = \(\dfrac{2}{2+1}\)= \(\dfrac{2}{3}\)
u4 (n = 3) = \(\dfrac{3}{3+1}\) = \(\dfrac{3}{4}\)
u5 (n = 4) = \(\dfrac{4}{4+1}\) = \(\dfrac{4}{5}\)
un (n = n - 1) = \(\dfrac{n-1}{n-1+1}\) = \(\dfrac{n-1}{n}\)
Do đề không cho n thuộc N* nên ta chọn n = 0
Chọn đáp án C