Giữa em và anh chỉ có thể là khoảng cách !!!
345 + 444 + 22 =
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
11 tháng 5 2019
Đáp án D
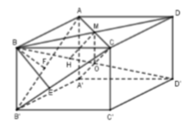
Phương pháp:
- Xác định các đoạn vuông góc chung của các cặp đường thẳng AB và B 'C, BC và AB '.
- Dựa vào giải thiết khoảng cách nhận xét tính chất của hai đáy ABCD và A 'B 'C 'D '.
- Xác định độ dài đoạn vuông góc chung của AC và BD '.
- Tính độ dài các cạnh của hình hộp chữ nhật và suy ra thể tích
CM
5 tháng 8 2017
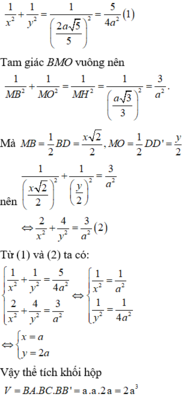
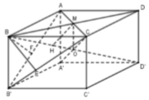
Gọi E, F lần lượt là hình chiếu của B lên B 'C và B 'A
Dễ thấy A B ⊥ ( B C C ' B ' ) nên A B ⊥ B E
Lại có B E ⊥ B ' C nên d A B , B ' C = B E = 2 a 5 5
Tương tự có d B C , A B ' = B F = 2 a 5 5
Xét các tam giác vuông BCB’ và BAB’ có: 1 B E 2 = 1 B F 2
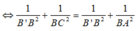
⇔ B C = B A hay ABCD là hình vuông
Suy ra B D ⊥ A C . Lại có A C ⊥ D D ' nên A C ⊥ ( B D D ' )
Gọi M = A C ∩ B D , O là tâm hình hộp và H là hình chiếu của M lên BD '
Khi đó A C ⊥ M H và M H ⊥ B D ' nên d A C , B D ' = M H = a 3 3
Đặt BA=BC=x, BB'=y ta có:
Tam giác BB 'C vuông nên
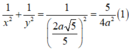
Tam giác BMO vuông nên
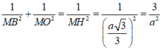
Mà M B = 1 2 B D = x 2 2 , M O = 1 2 D D ' = y 2
nên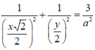 
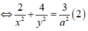
Từ (1) và (2) ta có:
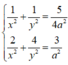
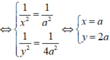
Vậy thể tích khối hộp
V = B A . B C . B B ' = a . a . 2 a = 2 a 3
Chọn đáp án D.
8 tháng 9 2015
đi bộ đi bộ đạp xe cách 1 cách 2
Gọi thời gian anh ta đi bộ thẳng đến sân vận động là t (giờ)
thời gian anh ta đi bộ về nhà là t' (giờ)
Vì thời gian đi cả 2 cách bằng nhau nên thời gian anh ta đạp xe là: t - t' (giờ)
Quãng đường anh ta đạp xe và tổng quãng đường anh ta đi bộ bằng nhau (đều bằng quãng đường từ nhà đến sân vận động)
Vì vận tốc đạp xe gấp 7 lần vận tốc đi bộ và Trên cùng một quãng đường, vận tốc tỉ lệ nghịch với thời gian nên
Tổng thời gian đi bộ gấp 7 lần thời gian đạp xe
=> t + t' = 7 (t - t') => 8t' = 6t => t/t' = 8/6 = 4/3
Với cùng một vận tốc, quãng đường tỉ lệ thuận với thời gian nên
Quãng đường anh từ chỗ anh ta đứng đến sân vận động / Quãng đường từ chỗ anh ta đứng đến nhà = 4/3
ĐS: 4/3
CM
18 tháng 6 2017
Đáp án C.
Giả sử các kích thước của hình hộp chữ nhật là A B = x , A D = y , A A ' = z . Trong đó x , y , z > 0 . Để giải bài toán, ta phân tích từng dữ kiện có trong đề bài.
1. Khoảng cách giữa hai đường thẳng AB và B'C bằng 2 a 5 5 .
Ta có
A B / / C D C D ⊂ A ' B ' C D A B ⊄ A ' B ' C D ⇒ A B / / A ' B ' C D ⇒ d A B ; B ' C = d A B ; A ' B ' C D
= d A ; A ' B ' C D = A H = 2 a 5 5 với H là hình chiếu của A trên .
Từ 1 A H 2 = 1 A A ' 2 + 1 A D 2 ⇒ 1 y 2 + 1 z 2 = 5 4 a 2 (1)
2. Khoảng cách giữa hai đường thẳng BC và AB' bằng 2 a 5 5 .
Tương tự, ta chứng minh được
B C / / A B ' C ' D ⇒ d B C ; A B ' = d B C ; A B ' C ' D
= B K = 2 a 5 5
với K là hình chiếu của B trên AB'.
Từ 1 B K 2 = 1 B A 2 + 1 B B ' 2 ⇒ 1 x 2 + 1 z 2 = 5 4 a 2 (2)
3. Khoảng cách giữa hai đường thẳng AC và BD' là a 3 3 .
Gọi O = A C ∩ B D ⇒ O là trung điểm của BD. Gọi I là trung điểm của DD' thì OI là đường trung bình của Δ B D D ' ⇒ O I / / B D ' ⇒ B D ' / / A C I
⇒ d B D ' ; A C = d B D ' ; A C I = d D ' ; A C I = d D ; A C I
Ta thấy DI, DA, DC đôi một vuông góc với nhau nên:
1 d 2 D ; A C I = 1 D A 2 + 1 D C 2 + 1 D I 2 = 1 D A 2 + 1 D C 2 + 4 D D ' ⇒ 1 x 2 + 1 y 2 + 4 z 2 = 3 a 2
(3)
Giải hệ phương trình gồm (1), (2) và (3) ta tìm được: x = y = z , z = 2 a .
Vậy thể tích của khối hộp chữ nhật đã cho là V = x y z = a . a .2 a = 2 a 3 (đvtt).