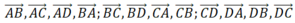Từ các điểm phân biệt A, B, C. Có bao nhiêu vectơ khác 0 được tạo ra? Hãy liệt kê các vectơ đó.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
30 tháng 9 2018
Các vectơ khác vectơ – không được lập ra từ 4 điểm đã cho là:
A B → ; A C → ; A D → ; B A → ; B C → ; B D → ; C A → ; C B → ; C D → ; D A → ; D B → ; D C →
Đáp án C
HH
1
AH
Akai Haruma
Giáo viên
15 tháng 9 2021
Lời giải:
$\overrightarrow{AB}, \overrightarrow{AC}, \overrightarrow{AD}, \overrightarrow{AE}$
$\overrightarrow{BA}, \overrightarrow{BC}, \overrightarrow{BD}, \overrightarrow{BE}$
$\overrightarrow{CA}, \overrightarrow{CB}, \overrightarrow{CD}, \overrightarrow{CE}$
$\overrightarrow{DA}, \overrightarrow{DB}, \overrightarrow{DC}, \overrightarrow{DE}$
$\overrightarrow{EA}, \overrightarrow{EB}, \overrightarrow{EC}, \overrightarrow{ED}$
HQ
Hà Quang Minh
Giáo viên
27 tháng 9 2023
Có thể tạo được 6 vecto theo yêu cầu đó là: \(\overrightarrow {AB} ,\overrightarrow {BA} ,\overrightarrow {AC} ,\overrightarrow {CA} ,\overrightarrow {BC,} \overrightarrow {CB} \)
CM
14 tháng 3 2018
Xét tập X = {A, B, C, D, E ; F}. Với mỗi cách chọn hai phần tử của tập X và sắp xếp theo một thứ tự ta được một vectơ thỏa mãn yêu cầu
Mỗi vectơ thỏa mãn yêu cầu tương ứng cho ta một chỉnh hợp chập 2 của 6 phần tử thuộc tập X.
Vậy số các vectơ thỏa mãn yêu cầu bằng số tất cả các chỉnh hợp chập 2 của 6, bằng
Chọn C.
CM
1 tháng 4 2017
Đáp án B.
Từ 2 điểm phân biệt có thể tạo được 2 vecto nên số vecto tạo ra được là 