Cho tam giác ABC , AB = 15cm, AC = 20cm ,BC = 25cm .I là trung điểm của AC
Chứng minh tam giác ABC vuông
Tính sinB + tanC
Tính BIC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
RS
25 tháng 10 2016
a) Ta có 252=152+202 hay BC2=AB2+AC2
=> ▲ABC vuông tại A
b) Xét ▲ABC vuông tại A có
SinB = \(\frac{AC}{BC}=\frac{20}{25}=\frac{4}{5}\)
TanC = \(\frac{AB}{AC}=\frac{15}{20}=\frac{3}{4}\)
=> SinB + TanC = \(\frac{4}{5}+\frac{3}{4}=\frac{31}{20}\)
c) I là trung điểm AC => AI = 10cm.
=> BI2 = 102+152= 325 => BI = \(5\sqrt{13}\)
Xét ▲ABI có TanI = \(\frac{3}{2}\)=> góc BIA = 56'18'
=> BIC = 180 - 56'18' = 123 độ 41 phút.
30 tháng 9 2021
\(a,AB^2+AC^2=15^2+20^2=625=25^2=BC^2\)
Vậy ABC là tam giác vuông tại A (pytago đảo)
\(b,\)Áp dụng HTL tam giác ABC vuông tại A, đường cao AH
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH^2=BH\cdot HC\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=9\left(cm\right)\\CH=\dfrac{AC^2}{BC}=12\left(cm\right)\\AH=\sqrt{9\cdot12}=6\sqrt{3}\left(cm\right)\end{matrix}\right.\)
Vì AM là phân giác nên \(\dfrac{MB}{MC}=\dfrac{AB}{AC}=\dfrac{3}{4}\Rightarrow MB=\dfrac{3}{4}MC\)
Mà \(MB+MC=BC=25\Rightarrow\dfrac{7}{4}MC=25\)
\(\Rightarrow MC=\dfrac{100}{7}\left(cm\right);MB=\dfrac{75}{7}\left(cm\right)\)
22 tháng 6 2023
a: Xét ΔBAI vuông tại A và ΔBAC vuông tại A có
BA chung
AI=AC
=>ΔBAI=ΔBAC
b: Xét ΔEIA và ΔFCA có
EI=FC
góc I=góc C
IA=CA
=>ΔEIA=ΔFCA
=>AE=AF
=>ΔAEF cân tại A
28 tháng 7 2023
a: BC=căn 15^2+20^2=25cm
AH=15*20/25=12cm
HC=AC^2/BC=20^2/25=16cm
Xét ΔACB vuông tại A có sin ACB=AB/BC=3/5
=>góc ACB=37 độ
b: Xét ΔHAB có HI/HA=HK/HB
nên IK//AB
=>KI vuông góc AC
Xét ΔCAK có
KI,AH là đường cao
KI cắt AH tại I
=>I là trực tâm
c: Xét ΔKBA và ΔIAC có
góc KBA=góc IAC
AB/AC=KB/IA=HB/HA
=>ΔKBA đồng dạng với ΔIAC
13 tháng 9 2023
a) Ta có: \(BD + DC = BC \Rightarrow DC = BC - BD = 25 - BD\)
Vì \(AD\) là phân giác của góc \(BAC\) nên theo tính chất đường phân giác ta có:
\(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} \Leftrightarrow \frac{{BD}}{{25 - BD}} = \frac{{15}}{{20}} \Leftrightarrow 20.BD = 15.\left( {25 - BD} \right) \Rightarrow 20.BD = 375 - 15.BD\)
\( \Leftrightarrow 20BD + 15BD = 375 \Leftrightarrow 35BD = 375 \Rightarrow BD = \frac{{375}}{{35}} = \frac{{75}}{7}\)
\( \Rightarrow DC = 25 - \frac{{75}}{7} = \frac{{100}}{7}\)
Vậy \(BD = \frac{{75}}{7}cm;DC = \frac{{100}}{7}cm\).
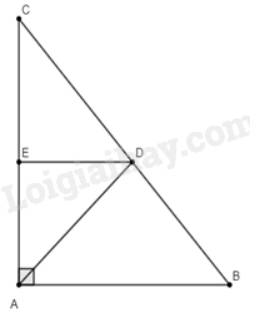
Vì \(DE//AB\) nên \(\frac{{DC}}{{BC}} = \frac{{DE}}{{AB}} \Rightarrow \frac{{\frac{{100}}{7}}}{{25}} = \frac{{DE}}{{15}} \Leftrightarrow DE = \frac{{100}}{7}.15:25 = \frac{{60}}{7}\) (hệ quả của định lí Thales).
Vậy \(BD = \frac{{75}}{7}cm;DC = \frac{{100}}{7}cm;DE = \frac{{60}}{7}cm\).
b) Xét tam giác \(ABC\) có:
\(B{C^2} = {25^2} = 625;A{C^2} = {20^2} = 400;A{B^2} = {15^2} = 225\)
\( \Rightarrow B{C^2} = A{C^2} + A{B^2}\)
Do đó, tam giác\(ABC\) là tam giác vuông tại \(A\).
c) Diện tích tam giác \(ABC\) là
\({S_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}.15.20 = 150\left( {c{m^2}} \right)\).
Xét tam giác \(ADB\) và tam giác \(ABC\) ta có:
\(\frac{{BD}}{{BC}} = \frac{{\frac{{75}}{7}}}{{25}} = \frac{3}{7}\) và có chung chiều cao hạ từ đỉnh \(A\). Do đó, diện tích tam giác \(ADB\) bằng \(\frac{3}{7}\) diện tích tam giác \(ABC\).
Diện tích tam giác \(ADB\) là:
\({S_{ADB}} = 150.\frac{3}{7} = \frac{{450}}{7}\left( {c{m^2}} \right)\).
Diện tích tam giác \(ACD\) là:
\({S_{ACD}} = {S_{ABC}} - {S_{ADB}} = 150 - \frac{{450}}{7} = \frac{{600}}{7}\)
Vì \(ED//AB \Rightarrow \frac{{CE}}{{AE}} = \frac{{CD}}{{BD}} = \frac{{\frac{{100}}{7}}}{{\frac{{75}}{{100}}}} = \frac{4}{3}\)
Xét tam giác \(ADE\) và tam giác \(DCE\) ta có:
\(\frac{{CE}}{{AE}} = \frac{4}{3}\) và hai tam giác này có chung đường cao hạ từ \(D\).
Do đó, \(\frac{{{S_{ADE}}}}{{{S_{DCE}}}} = \frac{4}{3}\).
Diện tích tam giác \(ADE\) là
\({S_{ADE}} = \frac{{600}}{7}:\left( {3 + 4} \right).4 = \frac{{2400}}{{49}}\left( {c{m^2}} \right)\)
\({S_{DCE}} = \frac{{600}}{7}:\left( {3 + 4} \right).3 = \frac{{1800}}{{49}}\left( {c{m^2}} \right)\).
13 tháng 9 2023
a: Xét ΔABC có AD là phân giác
nên DB/AB=DC/AC
=>DB/3=DC/4=(DB+DC)/(3+4)=25/7
=>DB=75/7cm; DC=100/7cm
Xét ΔABC có DE//AB
nên DE/AB=CD/CB
=>DE/15=100/7:25=4/7
=>DE=60/7cm
b: Xét ΔABC có BC^2=AB^2+AC^2
nen ΔABC vuông tại A
=>S ABC=1/2*15*20=10*15=150cm2
c: DB/DC=3/7
=>S ABD/S ACB=3/7
=>S ABD=150*3/7=450/7cm2
7 tháng 7 2015
a) Ta có: AB2 + AC2 = 202 + 152 = 625
BC2 = 252 = 625
nên AB2 + AC2 = BC2
Suy ra tam giác ABC vuông do định lí Pi-ta-go đảo
b) Áp dụng định lí Pitago trong tam giác vuông ACH được:
HC2 + HA2 = AC2
CH2 = 152 - 122
CH2 = 81
=> CH=9 (cm)
Áp dụng định lí Pitago trong tam giác vuông AHB được:
AH2 + BH2 = AB2
122 + BH2 = 202
=> BH2 = 202 - 122 = 256
=> BH=16 cm
KN
7 tháng 7 2015
Hình bạn tự kẻ nhé .
a) Ta có AB2+AC2 = 202+152= 625
Lại có BC2 = 252 = 625
=> Tam giác ABC vuông ( Py ta go )
b) Ta có AH là đường cao
=> Tam giác ABH và tam giác ACH vuông tại H
Áp dụng Py ta go vào tam giác vuông ACH ta được :
AC2=CH2+ AH2
=> 152 = CH2 + 122
=> CH2 = 152 - 122 = 81
=> CH = 9 ( cm)
=> BH = BC-CH = 25- 9 = 16 ( cm)