xét tính đúng sai của mỗi mệnh đề sau và phát biểu phủ định của nó :
\(\sqrt{5}-\sqrt{2}=\frac{1}{\sqrt{5}+\sqrt{3}}\)
b, 693 chia hết cho 3
c, \(\left(\sqrt{3-\sqrt{12}}\right)^2\)là số hữu tỷ
d, x=3 là 1 nghiệm của phương trình \(\frac{^{x^2-9}}{x-3}=0\)

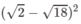
- mng giúp mình với ạ mình cần gấp
a) \(\sqrt{5}-\sqrt{2}=\frac{\left(\sqrt{5}-\sqrt{2}\right)\left(\sqrt{5}+\sqrt{2}\right)}{\left(\sqrt{5}+\sqrt{2}\right)}=\frac{5-2}{\sqrt{5}+\sqrt{2}}=\frac{3}{\sqrt{5}+\sqrt{2}}\)
Như vậy phát biểu a là sai
b) 693 chia hết cho 3 vài tổng các chữ số của nó là 6 + 9 + 3 = 18 chia hết cho 3, như vậy b đúng
c) \(3-\sqrt{12}< 3-\sqrt{9}=0\) vậy biểu thức \(\sqrt{3-\sqrt{12}}\) là không có nghĩa, c sai
d) Phương trình có biểu thức x -3 dưới mẫu nên để phương trình có nghĩa thì \(x\ne3\), vậy x = 3 không phải là nghiệm => d sai.