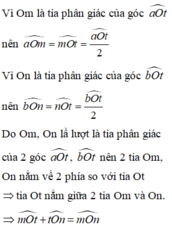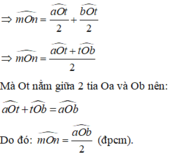Cho góc AOB = 100 độ , Ot là tia phân giác của góc AOB . Vẽ A'Ot' đối đỉnh với AOt . So sánh BOt' và BOA
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài làm
Vì Ot là tia phân giác của \(\widehat{AOB}\)
\(\Rightarrow\widehat{AOt}=\widehat{tOB}=\frac{\widehat{AOB}}{2}=\frac{100^0}{2}=50^0\)
Vì \(\widehat{A'Ot'}\) đối đỉnh với \(\widehat{AOt}\)
=>\(\widehat{A'Ot'}=50^0\)
Ta có: \(\widehat{tOB}+\widehat{BOA'}+\widehat{A'Ot'}=180^0\)( Vì \(\widehat{DOt'}\)là góc bẹp )
Hay \(50^0+\widehat{BOA'}+50^0=180^0\)
\(\Rightarrow\widehat{BOA'}=80^0\)
Lại có: \(\widehat{BOA'}+\widehat{A'Ot'}=80^0+50^0=130^0\)
Hay \(\widehat{BOt'}=130^0\)
Mà \(\widehat{AOB}=100^0\)
=> \(\widehat{BOt'}>\widehat{AOB}\left(130^0>100^0\right)\)
Vậy \(\widehat{BOt'}>\widehat{AOB}\)
# Học tốt #
Bài làm
Vì Ot là tia phân giác của \(\widehat{AOB}\)
\(\Rightarrow\widehat{AOt}=\widehat{tOB}=\frac{\widehat{AOB}}{2}=\frac{100^0}{2}=50^0\)
Vì \(\widehat{A'Ot'}\) đối đỉnh với \(\widehat{AOt}\)
=>\(\widehat{A'Ot'}=50^0\)
Ta có: \(\widehat{tOB}+\widehat{BOA'}+\widehat{A'Ot'}=180^0\)( Vì \(\widehat{DOt'}\)là góc bẹp )
Hay \(50^0+\widehat{BOA'}+50^0=180^0\)
\(\Rightarrow\widehat{BOA'}=80^0\)
Lại có: \(\widehat{BOA'}+\widehat{A'Ot'}=80^0+50^0=130^0\)
Hay \(\widehat{BOt'}=130^0\)
Mà \(\widehat{AOB}=100^0\)
=> \(\widehat{BOt'}>\widehat{AOB}\left(130^0>100^0\right)\)
Vậy \(\widehat{BOt'}>\widehat{AOB}\)
# Học tốt #

a)
b) ta có: góc aOt tù, góc a'Ot' nhọn
=> góc aOt > góc a'Ot'
=> góc aOt và góc a'Ot' không là cặp góc đối đỉnh ( định lí)

a: \(\widehat{a'Ob}+\widehat{aOb}=180^0\)
nên \(\widehat{a'Ob}=130^0\)

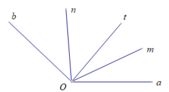
ta có \(Om\) là phân giác của \(\widehat{aOt}\) => \(\widehat{mOt}=\frac{\widehat{aOt}}{2}\)
tương tự ta có \(\widehat{nOt}=\widehat{\frac{bOt}{2}}\)
=> \(\widehat{mOt}+\widehat{nOt}=\frac{\widehat{aOt}+\widehat{bOt}}{2}=\widehat{\frac{aOb}{2}}\)
mà \(Ot\) nằm giữa \(Om\) và \(On\)
=> \(\widehat{mOn}=\widehat{mOt}+\widehat{nOt}=\widehat{\frac{aOb}{2}}\) (ĐPCM)