chứng tỏ rằng : 3x2 - 9/3x + 3 > 0 với mọi x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
10 tháng 7 2018
Điều kiện x ≠ 0 và x ≠ -3
Ta có:
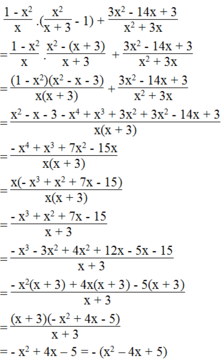
Vì x 2 - 4 x + 5 = x 2 - 4 x + 4 + 1 = x - 2 2 + 1 > 0 với mọi giá trị của x nên
- x 2 + 4 x - 5 = - x - 2 2 + 1 < 0 với mọi giá trị của x.
Vậy giá trị biểu thức luôn luôn âm với mọi giá trị x ≠ 0 và x ≠ -3
28 tháng 6 2019
TL:
Ta có:
\(x^2-3x+3=x^2-3x+2,25+0,75\)
=\(\left(x-1,5\right)^2+0,75\)
mà:\(\left(x-1,5\right)^2\ge0\forall x\in R\) ;0,75>0
\(\Rightarrow\left(x-1,5\right)^2+0,75\ge0,75>0\)
=>đpcm
hc tốt
KT
12 tháng 4 2018
\(9x^2-6x+3\)
\(=\left(9x^2-6x+1\right)+2\)
\(=\left(3x-1\right)^2+2\)
Vì \(\left(3x-1\right)^2\ge0\)
\(\Rightarrow\)\(\left(3x-1\right)^2+2>0\)
hay \(9x^2-6x+1>0\)
12 tháng 4 2018
Ta có :
\(9x^2-6x+3\)
\(=\left(9x^2-6x+1\right)+2\)
\(=\left(3x-1\right)^2+2\)
Mà \(\left(3x-1\right)^2\ge0\forall x\in R\)
\(\Rightarrow\left(3x-1\right)^2+2\ge2>0\forall x\in R\)
Vậy \(9x^2-6x+3>0\forall x\in R\)
NN
1
NC
1
MT
9 tháng 6 2015
a) x2-6x+10>0
<=>x2-6x+9+1>0
<=>(x-3)2+1>0(đúng với mọi x)
vậy x2-6x+10>0 với mọi x
b)x2-2x+y2+4y+6>0
<=>x2-2x+1y2+4y+4+1>0
<=>(x-1)2+(y+2)2+1>0 (với mọi x,y)
Vậy x2-2x+y2+4y+6>0 với mọi x,y
CM
23 tháng 1 2017
Biểu thức x x - 3 - x 2 + 3 x 2 x + 3 . x + 3 x 2 - 3 x - x x 2 - 9 xác định khi x – 3 ≠ 0,2x + 3 ≠ 0, x 2 - 3 x ≠ 0 và x 2 - 9 ≠ 0
Suy ra: x ≠ 3; x ≠ - 3/2 ; x ≠ 0; x ≠ 3 và x ≠ ± 3
Với điều kiện x ≠ 3; x ≠ - 3/2 ; x ≠ 0; x ≠ - 3, ta có:
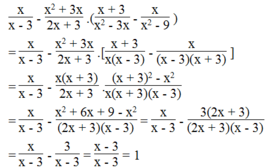
Vậy giá trị của biểu thức x x - 3 - x 2 + 3 x 2 x + 3 . x + 3 x 2 - 3 x - x x 2 - 9 bằng 1 khi x ≠ 3; x ≠ - 3/2 ; x ≠ 0; x ≠ - 3
sorry bn nhé! mik mới hok lớp 6 à
\(3x^2-\frac{9}{3}x+3=3\left(x^2-x+\frac{1}{4}\right)+\frac{9}{4}=3\left(x-\frac{1}{2}\right)^2+\frac{9}{4}\ge\frac{9}{4}>0\)