giúp em với ạ mai nộp rồi ạ
K
Khách
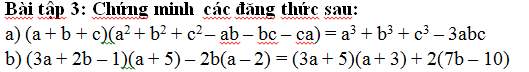
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DP
31 tháng 10 2021
xét tứ giác ANMP có
góc NAP = 90 độ ( AB vuông góc AC)
góc MPA = 90 độ (MP vuông góc AC)
Góc ANM = 90 độ (MN vuông góc AB)
=> tứ giác AMNP là hình chữ nhật
23 tháng 12 2023
Bài 6:
Xét ΔOAC vuông tại A và ΔOBD vuông tại B có
OA=OB
\(\widehat{AOC}=\widehat{BOD}\)(hai góc đối đỉnh)
Do đó: ΔOAC=ΔOBD
=>OC=OD
Bài 7:
a: Ta có: \(\widehat{DAB}+\widehat{BAC}+\widehat{CAE}=180^0\)
=>\(\widehat{DAB}+\widehat{CAE}+90^0=180^0\)
=>\(\widehat{DAB}+\widehat{CAE}=90^0\)
mà \(\widehat{DAB}+\widehat{DBA}=90^0\)
nên \(\widehat{DBA}=\widehat{CAE}\)
Xét ΔABD vuông tại A và D và ΔCAE vuông tại E có
AB=AC
\(\widehat{DBA}=\widehat{EAC}\)
Do đó: ΔABD=ΔCAE
b: ta có: ΔABD=ΔCAE
=>DB=AE và AD=CE
DB+CE=DA+AE=DE
9 tháng 11 2023
Gọi tia đối của tia AB là AE
=>AD là phân giác của \(\widehat{EAC}\)
Xét ΔABC có \(\widehat{EAC}\) là góc ngoài tại đỉnh A
nên \(\widehat{EAC}=\widehat{ABC}+\widehat{ACB}=80^0\)
AD là phân giác của góc EAC
=>\(\widehat{EAD}=\widehat{CAD}=\dfrac{\widehat{EAC}}{2}=\dfrac{80^0}{2}=40^0\)
\(\widehat{DAC}=\widehat{ACB}\left(=40^0\right)\)
mà hai góc này là hai góc ở vị trí so le trong
nên AD//BC
1 tháng 8 2023
a: góc OBA+góc OCA=90+90=180 độ
=>ABOC nội tiếp
b: góc OIE=góc OCE=90 độ
=>OICE là tứ giác nội tiếp
=>góc OEI=góc OCI
=>góc OEI=góc OCB
OBAC nội tiếp
=>góc OCB=góc OAB
=>góc OEI=góc OAB
=>góc OEI=góc OAI
=>OIAE nội tiếp
Mọi người ơi giúp em với ạ. Mai em phải nộp rồi. Mấy phần em đánh dấu đó mọi người. 
a: Ta có: \(a^3+b^3+c^3-3abc\)
\(=\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc\)
\(=\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2\right)-3ab\left(a+b+c\right)\)
\(=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ac\right)\)