Gía trị nhỏ nhất của hàm số y=\(\sin x-cos^2x+\dfrac{1}{2}\) là bao nhiêu
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CL
0
HP
2 tháng 8 2021
Đặt \(sin^24x=t\left(t\in\left[0;1\right]\right)\)
\(y=1-8sin^22x.cos^22x+2sin^42x\)
\(=1-2sin^24x+2sin^42x\)
\(\Rightarrow y=f\left(t\right)=1-2t+2t^2\)
\(y_{min}=min\left\{f\left(0\right);f\left(1\right);f\left(\dfrac{1}{2}\right)\right\}=\dfrac{1}{2}\)
\(y_{max}=max\left\{f\left(0\right);f\left(1\right);f\left(\dfrac{1}{2}\right)\right\}=1\)
12 tháng 9 2021
1, \(y=2-sin\left(\dfrac{3x}{2}+x\right).cos\left(x+\dfrac{\pi}{2}\right)\)
\(y=2-\left(-cosx\right).\left(-sinx\right)\)
y = 2 - sinx.cosx
y = \(2-\dfrac{1}{2}sin2x\)
Max = 2 + \(\dfrac{1}{2}\) = 2,5
Min = \(2-\dfrac{1}{2}\) = 1,5
2, y = \(\sqrt{5-\dfrac{1}{2}sin^22x}\)
Min = \(\sqrt{5-\dfrac{1}{2}}=\dfrac{3\sqrt{2}}{2}\)
Max = \(\sqrt{5}\)
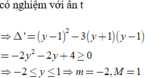
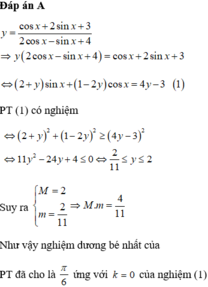
Lời giải:
Ta có: \(y=\sin x-\cos ^2x+\frac{1}{2}=\sin x-(1-\sin ^2x)+\frac{1}{2}\)
\(=\sin ^2x+\sin x-\frac{1}{2}=a^2+a-\frac{1}{2}\) (\(a=\sin x\in [-1;1]\) )
\(y'=2a+1=0\Leftrightarrow a=\frac{-1}{2}\)
Ta thấy:
\(y''=2>0\)
\(y(-1)=-\frac{1}{2}; y(1)=\frac{3}{2}; y(\frac{-1}{2})=\frac{-3}{4}\)
Do đó hàm số đạt min \(y=-\frac{3}{4}\) tại \(a=\sin x=\frac{-1}{2}\)