...
Đọc tiếp
25x2−40x+16
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
26 tháng 6 2017
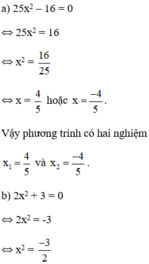
Phương trình vô nghiệm vì x 2 ≥ 0 với mọi x.
c) 4 , 2 x 2 + 5 , 46 x = 0
⇔ x.(4,2x + 5,46) = 0
⇔ x = 0 hoặc 4,2x + 5,46 = 0
+Nếu 4,2x + 5,46 = 0 ⇔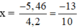 
Vậy phương trình có hai nghiệm
x
1
=
0
và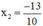 
d) 4 x 2 - 2 √ 3 x = 1 - √ 3 . ⇔ 4 x 2 - 2 √ 3 x – 1 + √ 3 = 0
Có a = 4; b’ = -√3; c = -1 + √3;
Δ ’ = b ' 2 – a c = ( - √ 3 ) 2 – 4 ( - 1 + √ 3 ) = 7 - 4 √ 3 = 4 – 2 . 2 . √ 3 + ( √ 3 ) 2 = ( 2 - √ 3 ) 2 .
Phương trình có hai nghiệm phân biệt:
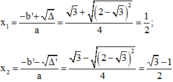
Cách 2: Sử dụng công thức nghiệm thu gọn với a, b, c
Kiến thức áp dụng
Phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức Δ = b2 – 4ac.
+ Nếu Δ > 0, phương trình có hai nghiệm phân biệt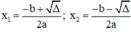 
+ Nếu Δ = 0, phương trình có nghiệm kép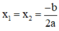 
;
+ Nếu Δ < 0, phương trình vô nghiệm.
ND
1
2 tháng 7 2021
\(B=\sqrt{\left(5x-3\right)^2}+\sqrt{\left(5x-4\right)^2}\ge\left|5x-3\right|+\left|4-5x\right|\ge5x-3+4-5x=1\).
Dấu "=" xảy ra khi và chỉ khi \(3\le5x\le4\Leftrightarrow\dfrac{3}{5}\le x\le\dfrac{4}{5}\)
17 tháng 10 2021
\(a,=\left(5x-1\right)^2\\ b,=\left(x+4\right)^2\\ c,=\left(4x+3y\right)^2\\ d,=\left(\dfrac{x}{4}+2y\right)^2\)
AT
1
27 tháng 7 2017
Ta có \(x^4+10x^3+32x^2+40x+16=\left(x^4+2x^3\right)+\left(8x^3+16x^2\right)+\left(16x^2+32x\right)+\left(8x+16\right)\)
\(=x^3\left(x+2\right)+8x^2\left(x+2\right)+16x\left(x+2\right)+8\left(x+2\right)\)
\(=\left(x+2\right)\left(x^3+8x^2+16x+8\right)=\left(x+2\right)\left(x+2\right)\left(x^2+6x+4\right)\)
\(=\left(x+2\right)^2\left(x^2+6x+4\right)\)
B
2
HQ
Hà Quang Minh
Giáo viên
25 tháng 7 2023
\(\left\{{}\begin{matrix}26⋮x\\x\ge13\end{matrix}\right.\Rightarrow x\in\left\{13;26\right\}\)
\(\left\{{}\begin{matrix}16⋮x\\x< 8\end{matrix}\right.\Rightarrow x\in\left\{1;2;4\right\}\)
\(\left\{{}\begin{matrix}18⋮x\\0< x< 40\end{matrix}\right.\Rightarrow x\in\left\{1;2;3;6;9;18\right\}\)
HQ
Hà Quang Minh
Giáo viên
25 tháng 7 2023
\(\left\{{}\begin{matrix}x⋮15\\30< x< 40\end{matrix}\right.\Rightarrow x\in\varnothing\)
\(\left\{{}\begin{matrix}x⋮12\\22\le5x\le50\end{matrix}\right.\Rightarrow x\in\varnothing\)
\(\left\{{}\begin{matrix}x⋮4\\16\le x\le36\end{matrix}\right.\Rightarrow x\in\left\{16;20;24;28;32;36\right\}\)
15 tháng 9 2021
a) \(=\left(x-2\right)^2\)
b) \(=\left(3x-2\right)^2\)
c) \(=\left(x-3y\right)^2\)
d) \(=\left(\dfrac{x}{2}+1\right)^2\)
e) \(=\left(x-4\right)^2\)
f) \(=\left(\dfrac{1}{2}xy^2+1\right)^2\)
g) \(=\left(x-1\right)\left(x+1\right)\)
h) \(=\left(5x-4\right)\left(5x+4\right)\)
VN
2
7 tháng 12 2017
\(25x^2+40x+16\)
\(=\left(5x\right)^2+2.5x.4+4^2\)
\(=\left(5x+4\right)^2\)
C
2
2 tháng 3 2020
X4-10x2-40x-16=O mình viết thiếu giải phép tình này hộ mình nhé
2 tháng 11 2021
Bài 1:
a) \(\Rightarrow3x^2+3x-2x^2-4x+x+1=0\)
\(\Rightarrow x^2=-1\left(VLý\right)\Rightarrow S=\varnothing\)
b) \(\Rightarrow\left(x-2020\right)\left(2x-1\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=2020\\x=\dfrac{1}{2}\end{matrix}\right.\)
c) \(\Rightarrow\left(x-10\right)\left(x+2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=10\\x=-2\end{matrix}\right.\)
d) \(\Rightarrow\left(x+4\right)^2=0\Rightarrow x=-4\)
e) \(\Rightarrow\left(x+6\right)\left(x-7\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-6\\x=7\end{matrix}\right.\)
f) \(\Rightarrow\left(5x-4\right)\left(5x+4\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{4}{5}\\x=-\dfrac{4}{5}\end{matrix}\right.\)
Bài 2:
a) \(\Rightarrow3x\left(x^2-4\right)=0\Rightarrow3x\left(x-2\right)\left(x+2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=2\\x=-2\end{matrix}\right.\)
b) \(\Rightarrow x\left(x-2\right)+5\left(x-2\right)=0\Rightarrow\left(x-2\right)\left(x+5\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=-5\end{matrix}\right.\)
25x2 - 40x + 16
=(5x)2 - 2.5x.4 + 42
=(5x -4)2