Cho 4 điểm A( 1;0), B(0;1), C(-1;0), D(0;-1)
a) CMR: ABCD là hình vuông
b) Tìm phương trình đường thẳng AB,BD,AC
c) Tìm phương trình đường thẳng đi qua trung điểm AB và CD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 9 2019
a/ Gọi \(D\left(a;0\right)\) \(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-9;3\right)\\\overrightarrow{AD}=\left(a-6;-3\right)\end{matrix}\right.\)
Do A; B; D thẳng hàng \(\Leftrightarrow\frac{a-6}{-9}=\frac{-3}{3}\Rightarrow a=15\) \(\Rightarrow D\left(15;0\right)\)
b/ \(\overrightarrow{AB}=\left(-1;5\right);\) \(\overrightarrow{AD}=\left(-2;10\right)\)
\(\Rightarrow\overrightarrow{AD}=2\overrightarrow{AB}\Rightarrow A,B,D\) thẳng hàng
NA
13 tháng 3 2022
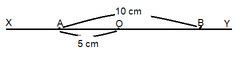
a. điểm O nằm giữa 2 điểm còn lại
b. ta có : OA + OB = AB
hay 5 + OB = 10
OB = 10 - 5 = 5(cm)
c. vì \(OA=OB=\dfrac{AB}{2}=5\left(cm\right)\)
nên O là trung điểm AB
30 tháng 10 2015
Chọn 1 trong 4 điểm ta vẽ được 3 đường thẳng đi qua 2 điểm
Cứ làm như thế với 4 điểm đó ta vẽ được : 4.3=12 đường thẳng
Vì mỗi đường thẳng được tính 2 lần
=> Số đường thẳng được tạo thành là 12:2=6
30 tháng 10 2019
Ta có: \(\overrightarrow {AD} \left( { - 2;10} \right),{\mkern 1mu} \overrightarrow {AB} \left( { - 1;5} \right) \Rightarrow \overrightarrow {AD} = 2\overrightarrow {AB} \)
\(\Rightarrow\) 3 điểm \(A,B,D\) thẳng hàng.
16 tháng 12 2023
Tọa độ trung điểm I của AB là:
\(\left\{{}\begin{matrix}x=\dfrac{1+1}{2}=1\\y=\dfrac{3-1}{2}=\dfrac{2}{2}=1\\z=\dfrac{5+1}{2}=\dfrac{6}{2}=3\end{matrix}\right.\)
vậy: I(1;1;3)
LM
1
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 1
\(\overrightarrow{DA}=\left(1;-1\right)\)
\(\overrightarrow{DC}=\left(4;4\right)=4\left(1;1\right)\)
\(\Rightarrow\overrightarrow{DC}=4\overrightarrow{DA}\) nên 4 điểm D, A, C thẳng hàng
AM
0
NK
0