Số nghiệm nguyên của bất phương trình \(\sqrt{5-2x}\)\(\le4\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\sqrt{5x-2}\le4\left(DK:x\ge\frac{2}{5}\right)\)
\(\Leftrightarrow5x-2\le16\Leftrightarrow5x\le18\Leftrightarrow x\le\frac{18}{5}\)
Vì \(x\in Z\)nên ta có : \(1\le x\le3\)
Vậy : Tập nghiệm nguyên của bất phương trình ; \(S=\left\{1;2;3\right\}\)
\(\sqrt{5x-2}\le4\left(DK:x\ge\frac{2}{5}\right)\)
\(\Leftrightarrow5x-2\le16\Leftrightarrow5x\le18\Leftrightarrow x\le\frac{18}{5}\)
Vì \(x\in Z\)nên ta có \(1\le x\le3\)
Vậy........................

\(\sqrt{x+3}-\sqrt{7-x}>\sqrt{2x-8}\)
⇔ \(\sqrt{x+3}>\sqrt{7-x}+\sqrt{2x-8}\)
⇔ \(\left\{{}\begin{matrix}4\le x\le8\\x+3>7-x+2x-8+2\sqrt{\left(7-x\right)\left(2x-8\right)}\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}4\le x\le8\\x+3>x-1+2\sqrt{\left(7-x\right)\left(2x+8\right)}\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}4\le x\le8\\4>2\sqrt{\left(7-x\right)\left(2x+8\right)}\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}4\le x\le8\\\sqrt{\left(7-x\right)\left(2x-8\right)}< 2\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}4\le x\le8\\-2x^2+22x-56< 2\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}4\le x\le8\\\left[{}\begin{matrix}x>\dfrac{11+\sqrt{5}}{2}\\x< \dfrac{11-\sqrt{5}}{2}\end{matrix}\right.\end{matrix}\right.\)
⇔ \(\left[{}\begin{matrix}4\le x< \dfrac{11-\sqrt{5}}{2}\\\dfrac{11+\sqrt{5}}{2}< x\le8\end{matrix}\right.\)
Các giá trị nguyên của x thỏa mãn là S = {4 ; 7 ; 8}
Ấy chết sai điều kiện XĐ rồi, bạn sửa lại điều kiện thôi nhé


Chọn A.
Phương pháp :
Cách giải : Trước hết ta giải biện luận phương trình
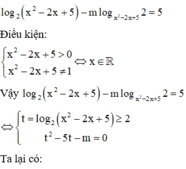
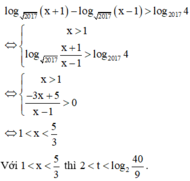

Vậy không có giá trị nguyên nào của m thỏa mãn.



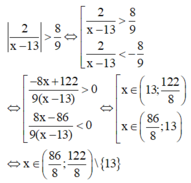
=>0<=5-2x<=16
=>0>=2x-5>=-16
=>5>=2x>=-11
=>5/2>=x>=-11/2
=>\(x\in\left\{2;1;0;-1;-2;-3;-4;-5\right\}\)
=>Số nghiệm nguyên là 8