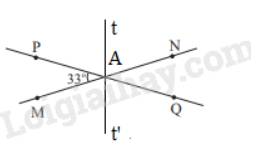
Cho hai đường thẳng MN và PQ cắt nhau tạo thành góc PAM= 33 độ
a. Tính số đo các góc còn lại
b. Vẽ At là tia phân giác của góc PAN. Hãy tính số đo của góc tAQ và góc MAQ. Vẽ At' là tia đối của tia At. Chứng tỏ rằng At' là tia phân giác của góc MAQ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: \(\widehat {PAM} = \widehat {QAN}\) ( 2 góc đối đỉnh) , mà \(\widehat {PAM} = 33^\circ \)nên \(\widehat {QAN} = 33^\circ \)
Vì \(\widehat {PAN} + \widehat {PAM} = 180^\circ \) ( 2 góc kề bù) nên \(\widehat {PAN} + 33^\circ = 180^\circ \Rightarrow \widehat {PAN} = 180^\circ - 33^\circ = 147^\circ \)
Vì \(\widehat {PAN} = \widehat {QAM}\)( 2 góc đối đỉnh) , mà \(\widehat {PAN} = 147^\circ \) nên \(\widehat {QAM} = 147^\circ \)
b)
Vì At là tia phân giác của \(\widehat {PAN}\) nên \(\widehat {PAt} = \widehat {tAN} = \frac{1}{2}.\widehat {PAN} = \frac{1}{2}.147^\circ = 73,5^\circ \)
Vì \(\widehat {tAQ} + \widehat {PAt} = 180^\circ \) ( 2 góc kề bù) nên \(\widehat {tAQ} + 73,5^\circ = 180^\circ \Rightarrow \widehat {tAQ} = 180^\circ - 73,5^\circ = 106,5^\circ \)
Vẽ At’ là tia đối của tia At, ta được \(\widehat {QAt'} = \widehat {PAt}\)( 2 góc đối đỉnh)
Ta có: \(\widehat {QAt'} = \widehat {MAt'} = \frac{1}{2}.\widehat {MAQ}\) nên At’ là tia phân giác của \(\widehat {MAQ}\)
Chú ý:
2 tia phân giác của 2 góc đối đỉnh là 2 tia đối nhau

a. Ta có: góc NOQ = POM= 60 ĐỘ
Ta có: MOP+ NOP= 180 độ(do kề bù)
60 + NOP= 180
NOP= 180- 60
Vậy: NOP= 120
Suy ra: MOQ= NOP= 120 độ(do so le trong)

a, Vì \(\widehat{mOp}\) đối đỉnh với \(\widehat{nOq}\) mà 2 góc đối đỉnh thì bằng nhau ,\(\widehat{mOp}\)=60độ \(\Rightarrow\) \(\widehat{nOq}\)= 60 độ
Vì tia Op và tia Oq đối nhau \(\Rightarrow\) \(\widehat{mOp}+\widehat{mOq}\)= 180 độ ( vì 2 góc đó kề bù )
\(\Rightarrow\)\(\widehat{mOq}\)= 180 độ - \(\widehat{mOp}\)
Hay : \(\widehat{mOq}\)=180 độ - 60 độ
Vậy :\(\widehat{mOq}\)= 120 độ
b, vì ot là tpg của góc mOp mà mOt = tOp = 1/2 x 60 = 30 độ mà góc nOq là góc đối đỉnh của mOp mà tia ot lại là tia đối của ot' \(\Rightarrow\)góc nOt' = t'Oq (=30 độ) và ot' nằm giữa vì ot nằm giữa om và op mà ot lại là tia đối ot' .
Vậy ot' là tpg của góc nOq
c, Các góc đối đỉnh là góc nhọn : góc nOp và mOq , góc tOm và nOt' ,góc tOp và t'Oq , góc mOpvaf nOq
đấy giải rồi đấy k đúng đê

a, MOP + NOP = 180 độ ( kề bù)
=> NOP =1 80 - NOP= 180 - 60 dộ = 120 dộ
Vì MOP và NOQ là hai góc đối đỉnh => MOP = NOQ = 60 độ
Vì NOP và MOQ là hai góc đối đỉnh => NOP = MOQ = 120 độ
b,OT là p/g MOP => POT = MOT = 1/2 POM = 1/2.60 độ = 30 độ
Vì POT và QOT' là hai góc đối đỉnh => POT = QOT" = 30 độ (1)
Vì MOT và NOT' là ..................... => MOT = NOT' = 30 độ (2)
Từ (1) và (2) => NOT' = QOT' = 30 độ => OT' là tia p/g NOQ
c, Các cặp góc đối đỉnh là góc nhọn :
(+) POT và QOT'
(+) MOT và NOT'
(+) POM và NOQ
a. + Vì \(PAM\) và \(MAQ\) là hai góc kề bù , ta có :
\(MAQ=180^0_{ }-33^0_{ }\)
\(MAQ=147^0_{ }\)
+Vì \(PAM\) đối đỉnh với \(NAQ\) nên \(NAQ=33^0_{ }\)
+ \(PAN\) đối đỉnh với \(MAQ\) nên \(PAN=147^0_{ }\)
b. +Vì \(AT\) là tia phân giác của \(PAN\) nên :
\(PAT=TAN=\dfrac{1}{2}PAN=\dfrac{147}{2}=73,5^0_{ }\)
Vì \(TAN\) và \(TAQ\) là hai góc kề bù, ta có :
\(TAN+NAQ=73,5^0_{ }+33^0_{ }\)
\(TAQ=106,5^0_{ }\)
Vì \(MAQ\) đối đỉnh với \(PAN\) nên \(MAQ=PAN\left(=147^0_{ }\right)\)
+ Vì \(AT\) là tia phân giác của \(PAN\) nên :
(1)\(PAT=TAN\)
Vì \(AT'\) là tia đối của tia \(AT\) nên :
(2)\(PTA=T'AQ\)
(3)\(TAN=MAT'\)
\(\Leftrightarrow\) Hai góc đối đỉnh
(4)Từ (1),(2),(3) suy ra \(MAT'=T'AQ\)
Do (4) và vì tia \(AT'\) nằm giữa hai tia \(AM-AQ\) (công nhận qua hình vẽ) nên \(AT'\) là tia phân giác của \(MAQ\).