CMR:
câu 1. ở doạn mạch gồm các điện trở mắc song song, điện trở tương đương ủa đoạn mạch luôn nhỏ hơn các điện trở thành phần
câu 2. thành lập công thức xác định điện trở tương đương của đoạn mạch gồm 3 điện trở mắc song song
giúp em vs ạ...!!!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo bài ra \(R_1//R_2//....//R_n\)
Ta có: \(\dfrac{1}{R_{tđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}+...+\dfrac{1}{R_n}\)
Suy ra: \(\dfrac{1}{R_{tđ}}>\dfrac{1}{R_1}\Leftrightarrow R_{tđ}< R_1\)
\(\dfrac{1}{R_{tđ}}>\dfrac{1}{R_2}\Leftrightarrow R_{tđ}< R_2;...;\dfrac{1}{R_{tđ}}>\dfrac{1}{R_n}\Leftrightarrow R_{tđ}< R_n\)
Vậy: \(R_{tđ}< R_1,R_2,...,R_n\left(đpcm\right)\)

Mình không biết có phải do bạn nhầm lẫn ko.
Nhưng theo mình thì đầy đủ ra là
Trong mạch điện có các điện trở mắc song song thì cường độ dòng điện đi qua mỗi điện trở thì tỉ lệ nghịch với điện trở đó
Ví dụ: R1//R2
vì mạch mắc song song
nên\(\dfrac{I_1}{I_2}=\dfrac{R_2}{R_1}\)
Hoặc có thể như này
công thức tính điện trở tương đương khi có 2 điện trở mắc song song
\(R_{tđ}=\dfrac{R_1R_2}{R_1+R_2}\)
Thì ta thấy điện trở tương đương đã tỉ lệ nghịch với tổng các điện trở thành phần
Ngoài ra công thức tính điện trở tương đương khi có nhiều điện trở dc mắc song song
\(\dfrac{1}{R_{tđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}+...+\dfrac{1}{R_n}\)
(còn nếu ko đúng thì mình cũng chịu nha. Nhưng bạn học thuộc các công thức mình ghi ra nha. Quan trọng đó!)

Áp dụng định luật Ôm cho đoạn mạch chỉ chứa điện trở và đưa và biểu thức (11.2) ta có
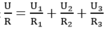
Suy ra điện trở tương đương của đoạn mạch song song
được tính bằng biểu thức sau :
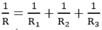

Điện trở tương đương của mạch mắc song song
A.nhỏ hơn mỗi điện trở thành phần.
B.bằng tổng các điện trở thành phần.
C.bằng mỗi điện trở thành phần.
D.lớn hơn mỗi điện trở thành phần
Câu 1:
Giả sử có n điện trở mắc song song với nhau:
Ta có: \(\dfrac{1}{R_{tđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}+...+\dfrac{1}{R_n}\)
Do R1;R2;...;Rn >0)
=> \(\dfrac{1}{R_{tđ}}>\dfrac{1}{R_1}\Leftrightarrow R_{tđ}< R_1\)
Tương tự ta chứng minh đ Rtđ < R2;....; Rtđ < Rn
Câu 2:
\(\dfrac{1}{R_{tđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}+\dfrac{1}{R_3}=\dfrac{R_2R_3+R_1R_3+R_1R_2}{R_1R_2R_3}\)
\(\Leftrightarrow R_{tđ}=\dfrac{R_1R_2R_3}{R_2R_3+R_1R_3+R_1R_3}\)