Một ô tô khối lượng 2 tấn đang xuống dốc dưới tác dụng của trọng lực biết dốc nghiêng so với mặt phẳng ngang một góc alpha 10 độ xác định hình chiếu của trọng lực trên hệ trục tọa độ Oxy biết Ox song song với mặt phẳng nghiêng và có chiều hướng xuống dưới Oy vuông góc với mawjpt phẳng nghiêng và có chiều hướng lên trên
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
Giản đồ vectơ các lực tác dụng lên thùng hàng:

b)
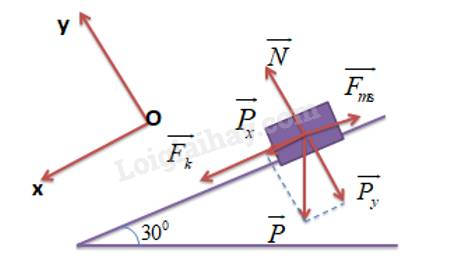
Ta có:
\({P_x} = P.\sin \alpha = 500.\sin {30^0} = 250N\)
\({P_y} = P.\cos \alpha = 500.\cos {30^0} = 500.\frac{{\sqrt 3 }}{2} = 250\sqrt 3 N\)
c)
Lực pháp tuyến của dốc lên thùng hàng không có tác dụng kéo thùng hàng xuống dốc vì nó cân bằng với thành phần \(\overrightarrow {{P_y}} \) của trọng lực.
d)
Chiếu các lực tác dụng lên trục Ox ta được:
\({F_k} - {F_{ms}} = ma \Leftrightarrow {F_k} - \mu N = ma\) (1)
Chiếu các lực tác dụng lên trục Oy ta được:
\(N - P.\cos \alpha = 0 \Leftrightarrow N = P.\cos \alpha = 250\sqrt 3 N\) (2)
Thay vào (1) ta được:
\(250 - \mu .250\sqrt 3 = \frac{{500}}{{10}}.2,00\)
\( \Leftrightarrow \mu = \frac{{150}}{{250\sqrt 3 }} = \frac{{\sqrt 3 }}{5} \approx 0,346\)
Vậy hệ số ma sát trượt giữa mặt dốc và thùng hàng là 0,346.

a. Áp dụng định lý động năng
A = W d B − W d A ⇒ A F → + A f → m s = 1 2 m v B 2 − 1 2 m v A 2
Công của lực kéo A F = F . s = 4000.100 = 4.10 5 ( J )
Công của lực ma sát
A f m s = − f m s . s = − μ N . s = − μ . m . g . s = − μ .2000.10.100 = − μ .2.10 6 ( J ) ⇒ 4.10 5 − μ .2.10 6 = 1 2 .2000.20 2 − 1 2 .2000.10 2 ⇒ μ = 0 , 05
b. Giả sử D làvị trí mà vật có vận tốc bằng không
Áp dụng định lý động năng
A = W d D − W d B ⇒ A P → + A f → m s = 1 2 m v D 2 − 1 2 m v B 2
Công trọng lực của vật
A P → = − P x . B D = − m g sin 30 0 . B D = − 10 4 . B D ( J )
Công của lực ma sát
A f m s = − f m s . B D = − μ N . B D = − μ . m . g cos 30 0 . B D = − 2000. B D ( J )
⇒ − 10 4 . B D − 2000. B D = 1 2 .2000.0 − 1 2 .2000.20 2 ⇒ B D = 33 , 333 ( m )
⇒ B C > B D nên xe không lên được đỉnh dốc.
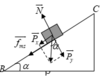
c. Áp dụng định lý động năng
A = W d C − W d B ⇒ A F → + A P → + A f → m s = 1 2 m v C 2 − 1 2 m v B 2
Công trọng lực của vật
A P → = − P x . B C = − m g sin 30 0 . B C = − 10 4 .40 = − 4.10 5 ( J )
Công của lực ma sát
A f m s = − f m s . B C = − μ N . B C = − μ . m . g cos 30 0 . B C = − 2000.40 = − 8.10 4 ( J )
Công của lực kéo
A F → = F . B C = F .40 ( J ) ⇒ F .40 − 4.10 5 − 8.10 4 = 0 − 1 2 .2000.20 2 ⇒ F = 2000 ( N )

để xe chuyển động đều (a=0)
\(\overrightarrow{F_k}+\overrightarrow{P}+\overrightarrow{N}=0\)
chiếu lên trục Ox song song với mặt phằng
Fk-sin\(\alpha\).P=0
\(\Rightarrow\)Fk=150N

a. Ta có
sin α = 1 2 ; cos α = 3 2
Công của trọng lực
A P = P x . s = P sin α . s = m g sin α . s A P = 2.10. 1 2 .2 = 20 ( J )
Công của lực ma sát
A f m s = − f m s . s = − μ N . s = − μ . m g cos α . s A f m s = − 1 3 .2.10. 3 2 .2 = − 20 ( J )
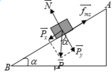
b. Áp dụng định lý động năng
A = W d B − W d A ⇒ A P → + A f → m s = 1 2 m v B 2 − 1 2 m v A 2 ⇒ 20 − 20 = 1 2 .2 v B 2 − 1 2 .2.2 2 ⇒ v B = 2 ( m / s )
c. Áp dụng định lý động năng
A = W d C − W d B ⇒ A f → m s = 1 2 m v C 2 − 1 2 m v B 2
Công của lực ma sát
A f m s = − f m s . s = − μ N . s = − μ . m g . s / = − μ .2.10.2 = − μ 40 ( J )
Dừng lại
v C = 0 ( m / s ) ⇒ − μ 40 = 0 − 1 2 .2.2 2 ⇒ μ = 0 , 1

Ta có: Chiều dài dốc là l=h√2 (vì nghiêng 45 độ nên l là cạnh huyền của △ vuông cân)
Công của trọng lực bằng công của lực ma sát là:
P.h = Fms1.l+Fms2.h= Fms2/2√ . h.2 + Fms2.h = 2Fms2.h ⇒ Fms2/P = 1/2
(Fms1 là lực ma sát trên dốc, Fms2 là lực ma sát trên mặt ngang)
Vậy ...

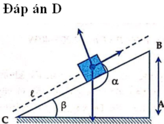
Công của trọng lực thực hiện từ lúc vật lên dốc đến lúc dừng lại trên dốc bằng: Ap=mgh
Với h là hiệu độ cao từ vị trí đầu đến vị trí cuối, tính theo hình ta có:
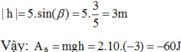

\(F_{ms}=\mu N=\mu.P.cos\alpha\)
\(\Leftrightarrow\mu=\dfrac{F_{ms}}{P.cos\alpha}=\dfrac{0,3P}{P.cos30^o}=\dfrac{\sqrt{3}}{5}\)
\(a=g\left(sin\alpha-\mu cos\alpha\right)=2\left(m\backslash s^2\right)\)
\(v^2-v_o^2=2as\)
\(\Leftrightarrow v=\sqrt{2as+v_o^2}=1\left(m\backslash s\right)\)