Cho đường tròn tâm O, đường kính AB và 1 dây AC bằng bán kính đường tròn . Tính các góc của tam giác ABC
giải giùm em với ạ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 8 2021
a) Ta có: ΔABC cân tại A
mà AH là đường cao ứng với cạnh BC
nên AH là đường trung tuyến ứng với cạnh BC
Ta có: AB=AC
nên A nằm trên đường trung trực của BC\(\left(1\right)\)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC\(\left(2\right)\)
Ta có: HB=HC
nên H nằm trên đường trung trực của BC(3)
Từ (1), \(\left(2\right),\left(3\right)\) suy ra A,O,H thẳng hàng
\(\Leftrightarrow A,O,H,D\) thẳng hàng
hay AD là đường kính của \(\left(O\right)\)
CM
5 tháng 12 2017
Đáp án C
Tam giác ABC có góc A là góc tù nên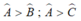 
Mà cạnh đối diện với góc A là cạnh BC .
Áp dụng định lí: trong 1 tam giác cạnh đối diện với góc lớn hơn thì lớn hơn ta được:
BC > AC và BC > AB
Vậy tam giác ABC có độ dài cạnh BC là lớn nhất nên dây BC gần tâm nhất.
Chưa thể kết luận dây nào xa tâm nhất.
2 tháng 6 2023
góc AEC=góc ADC=90 độ
=>AEDC nội tiếp
N là trung điểm của AC và R=AC/2
12 tháng 12 2023
a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
Xét ΔCAB vuông tại C có \(sinCAB=\dfrac{CB}{AB}\)
=>\(\dfrac{CB}{2R}=sin30=\dfrac{1}{2}\)
=>CB=R
Xét ΔCAB vuông tại C có \(CB^2+CA^2=AB^2\)
=>\(CA^2+R^2=\left(2R\right)^2=4R^2\)
=>\(CA^2=3R^2\)
=>\(CA=R\sqrt{3}\)
Chu vi tam giác ABC là:
\(C_{ABC}=CA+CB+AB=R+2R+R\sqrt{3}=R\left(3+\sqrt{3}\right)\)
b: Xét ΔCHA vuông tại H có \(sinCAH=\dfrac{CH}{CA}\)
=>\(\dfrac{CH}{R\sqrt{3}}=sin30=\dfrac{1}{2}\)
=>\(CH=\dfrac{R\sqrt{3}}{2}\)
Ta có: DA=2CH
=>\(DA=2\cdot\dfrac{R\sqrt{3}}{2}=R\sqrt{3}\)
Ta có: \(\widehat{DAC}+\widehat{CAB}=90^0\)
=>\(\widehat{DAC}=90^0-\widehat{CAB}=90^0-30^0=60^0\)
Xét ΔADC có \(AD=AC\left(=R\sqrt{3}\right)\) và \(\widehat{DAC}=60^0\)
nên ΔADC đều
=>\(\widehat{D}=60^0\)
Xét ΔOAC có OA=OC
nên ΔOAC cân tại O
=>\(\widehat{AOC}=180^0-2\cdot\widehat{OAC}=180^0-2\cdot30^0=120^0\)
c: Xét tứ giác DAOC có \(\widehat{DAO}+\widehat{DCO}+\widehat{ADC}+\widehat{AOC}=360^0\)
=>\(\widehat{DCO}+90^0+120^0+60^0=360^0\)
=>\(\widehat{DCO}=90^0\)
=>CD là tiếp tuyến của (O)
24 tháng 5 2015
Câu b.
Ta có tam giác EOH cân tại O
=> góc OEH=goc OHE
=> góc OHE= góc EHB (vì AHB cân Có HE là đường cao đồng thời là đường phân giác )
xét tứ giác EHDB nt
có gócEHB=gócEDB (cùng chắn EB)
=> góc OEH=gócEDB
Xét ttam giác EHD cân tại H ( H là trực tâm trong tam giác ABC cân)
có góc HED=góc HDE
mà góc HDE+gocEDB=90độ
=> góc HED+gocOEH=90độ
<=>OE vuông góc ED
câu c.
Xét tam giác BDA vuong tại D
AB2=AD2+DB2 (pytago)
AD2=AB2-BD2
AD2=169-25
AD2=144
AD=12
Xet tam giác OED vuông tại E có:
tam giác EHD cân => tam giác HEO cân ( trong tam giác vuông đường trung tuyến là một đoạn thẳng nối từ đỉnh của tam giác tới trung điểm của cạnh đối diện, sẽ chia ra 2 cạch = nhau )
Xét (O) có
O là trung điểm AH
=>OA=OH
Ta lại có H là trung điểm OD
do đó OA=OH=HD
mà AD=12
=>OA=OH=HD=12/3
=>OA=4cm
Xét \(\Delta\)ACB có AB là đường kính đường tròn ngoại tuyến
=>\(\Delta\)ACB vuông tại C ( đ/lý đường tròn )
=>\(\widehat{ACB}=90^o\)(t/c \(\Delta\)vuông)
Có OA=OC=R
mà AC=R(gt)
=>OA=OC=AC
=>\(\Delta\)AOC đều (đ/n \(\Delta\)đều)
=>\(\widehat{CAO}=60^o\)(t/c \(\Delta\)đều)
=>\(\widehat{CAB}=60^o\)(O\(\in\)AB)
Xét \(\Delta\)ACB vuông tại C có
\(\widehat{CAB}+\widehat{CBA}=90^o\)(2 góc phụ nhau trong \(\Delta\)vuông )
=>60o+\(\widehat{CBA}\)=90o(\(\widehat{CAB}=60^o\)
=>\(\widehat{CBA}\)=30o