Tìm phương trình nghiệm nguyeen của. x^2+y^2-2.(3x-5y)=11. x^2+4y^2=21+6x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) tách ra:
(x2 - 6x + 9) + (y2 +10y +25) - 34 = 11
(x -3)2 + (y + 5)2 = 45
do nghiêm nguyên lên bình phương cũng là số nguyên
45 = 9 +36
TH1:
(x-3)2 = 9 (y+5)2 = 36
x = 0 hoặc 6 y = 0 hoặc -10
TH2:
(x-3)2 = 36 (x+5)2 = 9
x=9 hoặc -3 y=-2 hoặc -8
mấy câu sau cũng dạng vậy

a) x2 + y2 - 2(3x - 5y) = 11
\(\Rightarrow\) x2 + y2 - 6x - 10y = 11
\(\Rightarrow\) (x2 - 6x + 9) + (y2 - 10y + 25) = 45
\(\Rightarrow\) (x - 3)2 + (y - 5)2 = 45
Các số chính phương nguyên bé hơn 45 là: 1; 4; 9; 16; 25; 36. Thay (x - 3)2 bằng các số đó ta được (y - 5)2 lần lượt là 44; 41; 36; 29; 20; 9, chỉ có 36 và 9 là số chính phương.
+ Nếu (x - 3)2 = 9 và (y - 5)2 = 36 thì x = 6 hoặc 0; y = 11 hoặc -1.
+ Nếu (x - 3)2 = 36 và (y - 5)2 = 9 thì x = 9 hoặc -3; y = 8 hoặc 2.

a)
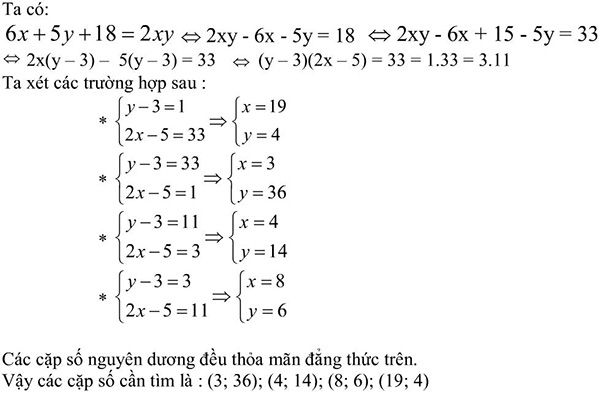
b)
Nhận thấy: x phải là số lẻ. Vì nếu x là số chẵn thì 3x^2 sẽ là số chẵn => 3x^2-4y^2 là số chẵn trong khi 13 là số lẻ
x là số lẻ => x có dạng x= 2k+1 với k thuộc Z
thay x=2k+1 vào phương trình ta có:
3(4k^2+4k+1) - 4y^2 = 13
<=> 6k^2+6k-2y^2=5
<=> 6k(k+1) = 5+2y^2
Dễ thấy vế trái là số chẵn trong khi vế phải là số lẻ => phương trình không có nghiệm nguyên => dpcm