Cho tam giác ABC nhọn nội tiếp (O) có H là trực tâm. M là điểm bất kì trên cung nhỏ BC. Gọi I, J lần lượt là hình chiếu của M trên AB, AC. Chứng minh I, J đi qua trung điểm của HM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 2 2020
Em kiểm tra lại đề bài . Gọi P, Q là hình chiếu của K trên BC và gì nữa vậy?
KN
13 tháng 7 2020
Gọi N là giao điểm của PQ và AH, gọi M là giao điểm của AH với (O). Khi đó dễ thấy tam giác PHK cân. Do AH//KP nên tứ giác KPMN là hình thang.
Lại có BPKQ nội tiếp nên suy ra được \(\widehat{QBK}=\widehat{ABK}=\widehat{ AMK}=\widehat{QPK}\)nên tứ giác KPMN nội tiếp. Do đó KPMN là hình thang cân. Do đó \(\widehat{PMH}=\widehat{PHM}=\widehat{KNM}\)nên KN//HP.
Do vậy tứ giác HPKN là hình bình hành. Từ đó ta có điều phải chứng minh.
1 tháng 12 2021
mik ko bt lm bài này bn à . mik thông minh lắm mấy bn mới ngu ấy
10 tháng 5 2023
góc MKC=góc MIC=90 độ
=>MCKI nội tiếp
=>góc MIK+góc MCK=180 độ
góc MIB+góc MHB=180 độ
=>MIBH nội tiếp
=>góc MIH=góc MBH
góc MIH+góc MIK
=180 độ-góc MCK+góc MBH
=180 độ
=>H,I,K thẳng hàng
CM
21 tháng 11 2019
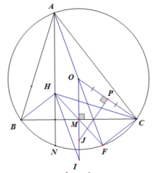
Ta có NHC = ABC (cùng phụ với HCB) (1)
Vì ABDC là tứ giác nội tiếp nên ABC = ADC (2)
Vì D và E đối xứng nhau qua AC nên AC là trung trực DE suy ra
∆ADC = ∆AEC (c.c.c) => ADC = AEC (3)
Tương tự ta có AEK = ADK
Từ (1), (2), (3) suy ra NHC = AEC => AEC + AHC = NHC + AHC = 180o
Suy ra AHCE là tứ giác nội tiếp => ACH = AEK = ADK (đpcm)
16 tháng 10 2019
Vẽ đường tròn ngoại tiếp (O) của \(\Delta\)ABC. Tiếp tuyến tại B và C của (O) cắt nhau ở T.
Gọi HM cắt đường tròn (O) tại hai điểm K và D (K thuộc cung lớn BC), AH cắt (O) và (AEF) tại L và I (khác A).
Dễ chứng minh AD là đường kính của (O) và ^AKP = 900, suy ra K thuộc đường tròn (AEF)
Từ đó \(\Delta\)EKF ~ \(\Delta\)CKB (g.g). Dễ thấy ^IFE = ^IAE = ^LBC; ^IEF = ^IAF = ^LCB suy ra \(\Delta\)EIF ~ \(\Delta\)CLB
Do vậy \(\frac{KF}{KE}.\frac{IE}{IF}=\frac{KB}{KC}.\frac{LC}{LB}=\frac{KB}{KC}.\frac{DB}{DC}=\frac{KB}{KC}.\frac{DB}{BM}.\frac{CM}{DC}=\frac{KB}{KC}.\frac{KC}{KM}.\frac{KM}{KB}=1\)
Suy ra 2 tứ giác KFIE và KBLC điều hòa, dẫn đến K,I,S thẳng hàng và K,L,T thẳng hàng
Theo tính đồng dạng thì \(\Delta\)KIF ~ \(\Delta\)KLB và \(\Delta\)KFS ~ \(\Delta\)KBT kéo theo \(\Delta\)IKL ~ \(\Delta\)SKT (~\(\Delta\)FKB)
Vậy ST // IL, mà IL vuông góc với BC, T thuộc trung trực của BC nên S thuộc trung trực của BC hay SB = SC (đpcm).