Tìm cực trị của hàm số
Y=x3-6x2+12x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
11 tháng 12 2019
Chọn D
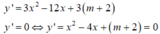
Hàm số có 2 điểm cực trị x1; x2 ⇔ Δ' > 0 ⇔ 4 - (m + 2) > 0 ⇔ m < 2
Chia y cho y’ ta được :
Suy ra : Phương trình đường thẳng đi qua hai điểm cực trị là: y = (m - 2)(2x + 1).
Điểm cực trị tương ứng : A(x1;(m - 2)(2x1 + 1)) và B(x2;(m - 2)(2x2 + 1))
Có:
CM
30 tháng 3 2018
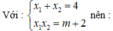
Chọn D
Hàm số có 2 điểm cực trị x 1 , x 2
Chia y cho y’ ta được :
Điểm cực trị tương ứng :
Với x 1 + x 2 = 4 x 1 x 2 = m + 2 nên y 1 y 2 = ( m - 2 ) 2 ( 4 m + 17 )
Hai cực trị cùng dấu ⇔ y 1 y 2 > 0
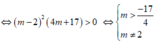
Kết hợp đk : - 17 4 < m < 2
PT
1
CM
11 tháng 7 2018
Đáp án C
Ta có y ' = - 3 x 2 + 12 x + 15 ; y ' = 0 ⇔ [ x = - 1 x = 5 ⇒ cực tiểu là y(-1) = 2
CM
13 tháng 9 2019
Đáp án D.
Ta có y ' = 6 x 2 + 6 1 - m x + 6 m - 2 .
Hàm số có điểm cực trị x 0 = 2 ⇒ 6 . 2 2 + 6 . 1 - m . 2 + 6 . m - 2 = 0 ⇔ m = 4 .
Với m = 4 hàm số có thêm một điểm cực trị x 1 = m - 2 2 = 1 .
Hàm số đã cho trở thành y = 2 x 3 - 9 x 2 + 12 x + n .
Hàm số này có hai cực trị là y 0 = y 2 = n + 4 và y 1 = y 1 = n + 5 .
Hàm số có hai cực trị đều dương ⇔ n + 4 > 0 n + 5 > 0 ⇔ n > - 4
Vậy giá trị nguyên nhỏ nhất của n là ‒3. Do đó giá trị nhỏ nhất của m + n (với m , n nguyên) là 4 + - 3 = 1 . Chọn đáp án D.
CM
17 tháng 11 2017
Chọn đáp án A
Hàm số đã cho có 5 điểm cực trị khi hàm số y = x 3 - 6 x 2 + m x - 1
có hai điểm cực x 1 , x 2 thỏa mãn x 1 > 0 , x 2 > 0
⇔ Phương trình y ' = 3 x 2 - 12 x + m = 0 có hai nghiệm dương phân biệt
Khi đó
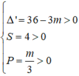
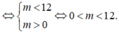
Do m ∈ 1 ; 2 ; 3 ; . . ; 11
Vậy có 11 giá trị m nguyên thỏa mãn yêu cầu bài toán
CM
15 tháng 10 2019
Đáp án A
y = x 3 − 6 x 2 + m x − 1 ( 1) là hàm chẵn nên đồ thị hàm số đối xứng với nhau qua trục tung.
Đặt x = t , t ≥ 0 . Khi đó :
y = t 3 − 6 t 2 + m t − 1 (*)
Để hàm số (1) có 5 cực trị <=> hàm số (*) có 2 cực trị dương
⇔ y ' = 0 có 2 nghiệm dương phân biệt
⇔ 3 t 2 − 12 t + m = 0 có 2 nghiệm dương phân biết
⇔ Δ ' = 36 − 3 m > 0 12 2.3 > 0 3. m > 0 ⇔ 0 < m < 12
CM
23 tháng 8 2017
+ Ta có đạo hàm y’ = 3x2- 12x+ 3( m+ 2)
Phương trình y’ = 0 khi 3x2- 12x+ 3( m+ 2) = 0
+ Hàm số có 2 điểm cực trị x1; x2 ⇔ Δ’ > 0 ⇔ m < 2
+ Chia y cho y’ ta được :y= 1/3.y’( x-2) + (m-2) (2x+ 1)
Tọa độ 2 điểm cực trị tương ứng : A( x1 ; ( m-2) ( 2x1+ 1) ) và B( x2 ; ( m-2) ( 2x2+ 1) )
+ ta có ; y1.y2= ( m-2) 2( 4x1x2+ 2( x1+ x2) + 1)
Với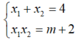 
nên: y1y2= ( m-2) 2( 4m+ 17)
Hai cực trị cùng dấu khi và chỉ khi y1.y2> 0 hay ( m-2) 2( 4m+ 17) > 0
⇔ m > - 17 4 m ≠ 2
Kết hợp điều kiện ta được : -17/4< m< 2; mà m nguyên nên m= -4; -3; ...0; 1
Có tất cả 6 giá trị nguyên của m thỏa mãn đầu bài.
Chọn C.
ta có : \(y'=\left(x^3-6x^2+12x\right)=3x^2-12x+12\)
\(\Rightarrow y'=0\Leftrightarrow3x^2-12x+12\Leftrightarrow x=2\)
vậy cực trị của hàm số \(y=x^3-6x^2+12x\) là \(2\)