Cho một bảng gồm 9 ô như hình dưới đây:
| 1 | ||
| 3 | 7 | |
| 9 |
Hãy điền các ô của bảng các số tự nhiên từ 1 đến 9 (Mỗi số chỉ được viết một lần) sao cho tổng các
số ở mỗi hàng,mỗi cột ,mỗi đường chéo đều bằng nhau.(tìm 7 đáp án khác nhau)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử có thể điền được theo yêu cầu bài toán (Bạn Nhi nói đúng).
Tổng các số tự nhiên liên tiếp từ 1 đến 8 là : 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36.
Mỗi dòng điền các số tự nhiên liên tiếp từ 1 đến 8 nên tổng các số trên 3 dòng trong bảng ô vuông đó là : 36 x 3 = 108. Vì tổng các số ở 8 cột đều bằng nhau nên tổng tất cả các số trong bảng ô vuông phải là một số chia hết cho 8. Nhưng 108 không chia hết cho 8 nên điều giả sử ở trên là sai tức là bạn Nhi nói sai và bạn Tín nói đúng.

Chọn đáp án C.
Số cách sắp xếp 9 chữ số đã cho vào ô vuông bằng n(Ω)=9!
Ta có: A là biến cố: “tồn tại một hàng hoặc một cột gồm ba số chẵn”.
Do có 4 số chẵn (2, 4, 6, 8) nên A là biến cố: “có đúng một hàng hoặc một cột gồm 3 số chẵn”.
Ta tính n A :
Chọn 4 ô điền số chẵn:
Ø Chọn một hàng hoặc một cột thì có 6 cách.
Ø Chọn một ô còn lại có 6 cách.
Điền 4 số chẵn vào 4 ô trên có 4! cách.
Điền 5 số lẻ vào 5 ô còn lại có 5! Cách.
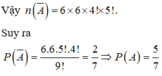

Chọn B
Ta có ![]()
Xét A ¯ : Có ít nhất một hàng hoặc một cột chỉ toàn số chẵn.
Vì chỉ có 4 số chẵn là 2, 4, 6, 8 nên chỉ có thể có đúng một hàng hoặc đúng một cột chỉ toàn các số chẵn. Để điền như vậy cần chọn một trong số ba hàng hoặc ba cột rồi chọn 3 số chẵn xếp vào hàng hoặc cột đó, 6 số còn lại xếp tùy ý. Do đó ![]()
Vậy ![]()

Chọn C
Số phần tử của không gian mẫu ![]()
Gọi A là biến cố “mỗi hàng, mỗi cột bất kì đều có ít nhất một số lẻ”.
A ¯ là biến cố “có một hàng, hoặc một cột đều là số chẵn”
Vì có 4 số chẵn nên chỉ có một hàng hoặc một cột xếp toàn số chẵn
Có 6 cách chọn ra một hàng hoặc hoặc một cột để xếp 3 số chẵn.
Có 6 cách chọn một ô không thuộc hàng đó để xếp tiếp 1 số chẵn nữa
Có 4! cách xếp 4 số chẵn và 5! xếp 5 số lẻ.
Vậy xác xuất ![]() .
.
Ta thấy 3 + 7 = 1 + 9 = 10
Do đó ô đứng giữa sẽ là một trong cách số 2,4,5,6,8
Thử từng trường hợp thì rút ra kết quả
Bạn thử tiếp các trường hợp trên , mình chỉ nêu ra ví dụ điển hình