√9x2−6x 1 tìm x để căn thức có nghĩa
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 9 2017
có \(9x^2-6x+1=\left(3x-1\right)^2\)
lại có \(\left(3x-1\right)^2\)>= 0 với mọi x
\(\Rightarrow\sqrt{9x^2-6x+1}\)luôn xác định với mọi x
3 tháng 9 2017
căn thức trên có nghĩa khi : 9x2 -6x +1 > 0
<=> giải pt trên ta có x > 1/3
Vậy x > 1/3 thì căn thức có nghiệm
PT
0
29 tháng 12 2021
a: \(M=\dfrac{2\left(1-3x\right)\left(1+3x\right)}{3x\left(x+2\right)}\cdot\dfrac{3x}{2\left(1-3x\right)}=\dfrac{3x+1}{x+2}\)
20 tháng 6 2023
8:
a: M(x)=x^4+2x^2+1
N(x)=x^4+2x^2-3x-14
P(x)=M(x)-N(x)=3x+15
P(x)=0
=>3x+15=0
=>x=-5
b: M(x)=x^2(x^2+1)+1>0
=>M(x) vô nghiệm
PT
1
H
26 tháng 6 2023
\(\sqrt{x-2\sqrt{x-1}}\)
\(\Rightarrow\left\{{}\begin{matrix}x-2\sqrt{x-1}\ge0\\x-1\ge0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x\ge2\sqrt{x-1}\\x\ge1\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x^2\ge4\left(x-1\right)^2\\x\ge1\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x^2-4x^2+8x-4\ge0\\x\ge1\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}\dfrac{2}{3}\le x\le2\\x\ge1\end{matrix}\right.\\ \Rightarrow\dfrac{2}{3}\le x\le2\)
PB
3
24 tháng 7 2017
\(\sqrt{-\left|3-x\right|}\)
Để căn thức trên có nghĩa thì :
\(\sqrt{-\left|3-x\right|}\)\(\ge0\)
TL
24 tháng 7 2017
Để căn thức trên có nghĩa.
Mà căn của 1 số ko thể âm.
=>-|3-x| dương hoặc =0.
Loại trường hợp dương vì GTTĐ của 1 số ko thể nhỏ hơn 0.
=>-|3-x|=0.
=>|3-x|=0.
=>3-x=0.
=>x=3.
Vậy x=3
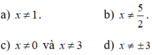
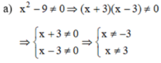
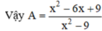
Để căn thức có nghĩa khi \(9x^2-6x+1\ge0\Leftrightarrow\left(3x-1\right)^2\ge0\Leftrightarrow x\ge\frac{1}{3}\)