1) cho Δ abc vuông ở a . Đường cao ah. Biết ab=3cm,ac=4cm
a) tính bc,ah,bh,hc.
b) giả sử ho vuông góc với ab ở o. Hn vuông góc với ac ở n. Tính on.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 10 2021
a, Áp dụng PTG: \(BC=\sqrt{AB^2+AC^2}=5\left(cm\right)\)
b, Vì AI là trung tuyến ứng ch BC nên \(AI=\dfrac{1}{2}BC=2,5\left(cm\right)\)
Áp dụng HTL: \(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{12}{5}=2,4\left(cm\right)\)
KL
9 tháng 7 2016
Áp dụng định lí Pi ta go vào tam giác vuông AHB ta có
\(AB^2=AH^2+BH^2\) =>\(BH^2=AB^2-AH^2\)=>\(BH=\sqrt{30^2-24^2}=\sqrt{324}=18\left(cm\right)\)
Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông ta có
\(AH^2=BH.CH\)=>\(HC=\frac{AH^2}{BH}\)=>\(HC=\frac{24^2}{18}=\frac{576}{18}=32\left(cm\right)\)
Ta có \(BC=HC+HB\) => \(BC=32+18=50\left(cm\right)\)
Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông ta có
\(AC^2=BC.HC\)
=>\(AC=\sqrt{BC.HC}=\sqrt{50.32}=\sqrt{1600}=40\left(cm\right)\)*Chỗ này bạn dùng Pitago tính cũng được nha*
KL
9 tháng 7 2016
Ta có góc HBD+ góc ABH = 90 độ mà góc ACH + góc ABH = 90 độ
=> góc HBD = góc ACH
Xét tam giác BHD và tam giác CHA có
góc BHD = góc CHA = 90 độ
góc HBD = góc ACH (chứng minh trên)
Do đó tam giác BHD ~ tam giác CHA
=> \(\frac{BD}{BH}=\frac{AC}{HC}\)
=>\(BD=\frac{AC.BH}{HC}=\frac{18.40}{32}=\frac{720}{32}=22,5\left(cm\right)\)
19 tháng 10 2021
c: Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
PN
0
29 tháng 8 2021
a: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HE là đường cao ứng với cạnh huyền BA, ta được:
\(AE\cdot AB=AH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HF là đường cao ứng với cạnh huyền CA, ta được:
\(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
hay \(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Xét ΔAEF vuông tại A và ΔACB vuông tại A có
\(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Do đó: ΔAEF\(\sim\)ΔACB
1 tháng 11 2023
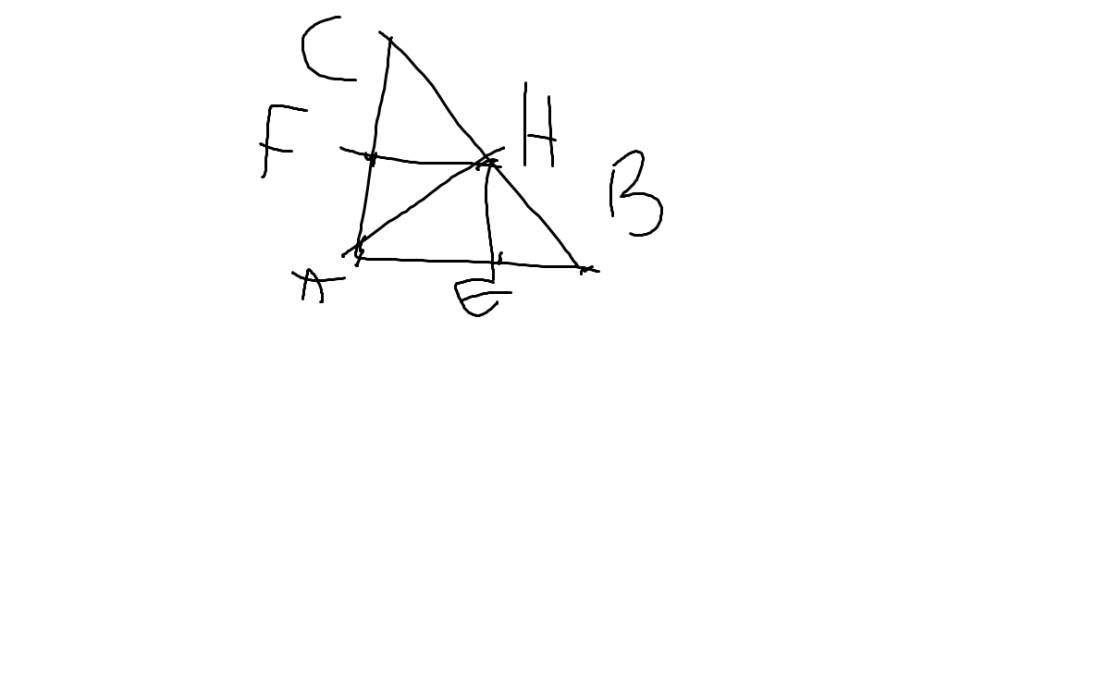
a: ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
=>HC*4=3^2=9
=>HC=2,25(cm)
BC=BH+CH
=2,25+4
=6,25(cm)
XétΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AB^2=2,25\cdot6,25\\AC^2=4\cdot6,25\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AB=\sqrt{2,25\cdot6,25}=3,75\left(cm\right)\\AC=\sqrt{25}=5\left(cm\right)\end{matrix}\right.\)
Xét ΔABC vuông tại A có
\(sinC=\dfrac{AB}{BC}=\dfrac{3}{5}\)
nên \(\widehat{C}\simeq37^0\)
=>\(\widehat{B}=90^0-37^0=53^0\)
b: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
=>AEHF là hình chữ nhật
=>HA=EF=3(cm)
c: ΔAHB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
BC2=AB2+AC2BC2=AB2+AC2
⇔BC2=32+42=25⇔BC2=32+42=25
hay BC=5(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
AH⋅BC=AB⋅ACAH⋅BC=AB⋅AC
⇔AH⋅5=3⋅4=12⇔AH⋅5=3⋅4=12
hay AH=2,4(cm)