Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1.
\(a,\left(-xy\right)\left(-2x^2y+3xy-7x\right)\)
\(=2x^3y^2-3x^2y^2+7x^2y\)
\(b,\left(\dfrac{1}{6}x^2y^2\right)\left(-0,3x^2y-0,4xy+1\right)\)
\(=-\dfrac{1}{20}x^4y^3-\dfrac{1}{15}x^3y^3+\dfrac{1}{6}x^2y^2\)
\(c,\left(x+y\right)\left(x^2+2xy+y^2\right)\)
\(=\left(x+y\right)^3\)
\(=x^3+3x^2y+3xy^2+y^3\)
\(d,\left(x-y\right)\left(x^2-2xy+y^2\right)\)
\(=\left(x-y\right)^3\)
\(=x^3-3x^2y+3xy^2-y^3\)
2.
\(a,\left(x-y\right)\left(x^2+xy+y^2\right)\)
\(=x^3-y^3\)
\(b,\left(x+y\right)\left(x^2-xy+y^2\right)\)
\(=x^3+y^3\)
\(c,\left(4x-1\right)\left(6y+1\right)-3x\left(8y+\dfrac{4}{3}\right)\)
\(=24xy+4x-6y-1-24xy-4x\)
\(=\left(24xy-24xy\right)+\left(4x-4x\right)-6y-1\)
\(=-6y-1\)
#Toru

\(\dfrac{M}{3}=\dfrac{x^2+y^2-xy}{x^2+y^2+xy}=\dfrac{3\left(x^2+y^2+xy\right)-2\left(x^2+y^2+2xy\right)}{x^2+y^2+xy}=3-\dfrac{2\left(x+y\right)^2}{x^2+y^2+xy}\le3\)
\(\Rightarrow M\le9\)
\(M_{max}=9\) khi \(\left\{{}\begin{matrix}x+y=0\\x^2+y^2+xy=3\end{matrix}\right.\) \(\Rightarrow\left(x;y\right)=\left(-\sqrt{3};\sqrt{3}\right);\left(\sqrt{3};-\sqrt{3}\right)\)
\(\dfrac{M}{3}=\dfrac{x^2+y^2-xy}{x^2+y^2+xy}=\dfrac{\dfrac{1}{3}\left(x^2+y^2+xy\right)+\dfrac{2}{3}\left(x^2+y^2-2xy\right)}{x^2+y^2+xy}=\dfrac{1}{3}+\dfrac{2\left(x-y\right)^2}{3\left(x^2+y^2+xy\right)}\ge\dfrac{1}{3}\)
\(\Rightarrow M\ge1\)
\(M_{min}=1\) khi \(\left\{{}\begin{matrix}x-y=0\\x^2+y^2+xy=3\end{matrix}\right.\) \(\Rightarrow x=y=\pm1\)

\(1,Sửa:A=4x^4+4x^2y+y^2+2=\left(2x^2+y\right)^2+2\ge2\\ A_{min}=2\Leftrightarrow2x^2+y=0\Leftrightarrow x^2=-\dfrac{y}{2}\\ 2,B=\left(x+y\right)^2+\left(y+1\right)^2+12\ge12\\ B_{min}=12\Leftrightarrow\left\{{}\begin{matrix}x=-y=1\\y=-1\end{matrix}\right.\)

a) Đây không phải là phương trình đường tròn do có \(xy\).
b) Vì \({a^2} + {b^2} - c = {1^2} + {2^2} - 5 = 0\)nên phương trình đã cho không là phương trình tròn.
c) Vì \({a^2} + {b^2} - c = {\left( { - 3} \right)^2} + {4^2} - 1 = 24 > 0\)nên phương trình đã cho là phương trình tròn có tâm \(I\left( { - 3;4} \right)\) và bán kính \(R = \sqrt {{a^2} + {b^2} - c} = 2\sqrt 6 \).

\(\dfrac{x^2+y^2}{2}\ge xy\Rightarrow-xy\ge-\dfrac{x^2+y^2}{2}\)
\(\Rightarrow4=x^2+y^2-xy\ge x^2+y^2-\dfrac{x^2+y^2}{2}=\dfrac{x^2+y^2}{2}\)
\(\Rightarrow x^2+y^2\le8\)
\(C_{max}=8\) khi \(x=y=\pm2\)
\(x^2+y^2\ge-2xy\Rightarrow-xy\le\dfrac{x^2+y^2}{2}\)
\(4=x^2+y^2-xy\le x^2+y^2+\dfrac{x^2+y^2}{2}=\dfrac{3}{2}\left(x^2+y^2\right)\)
\(\Rightarrow x^2+y^2\ge\dfrac{8}{3}\)
\(C_{min}=\dfrac{8}{3}\) khi \(\left(x;y\right)=\left(-\dfrac{2}{\sqrt{3}};\dfrac{2}{\sqrt{3}}\right);\left(\dfrac{2}{\sqrt{3}};-\dfrac{2}{\sqrt{3}}\right)\)

\(P=\dfrac{x^2-6xy+6y^2}{x^2-2xy+y^2}=\dfrac{-3\left(x^2-2xy+y^2\right)+4x^2-12xy+9y^2}{x^2-2xy+y^2}\)
\(=-3+\left(\dfrac{2x-3y}{x-y}\right)^2\ge-3\)
\(P_{min}=-3\) khi \(2x=3y\)

Tu x+3y=1nen x=1-3y Ta co A=(1-3y)2+y2=1-6y+9y2+y2 =10y2-6y+1 =10(y2-3/5y+1/10) =10(y2-2x3/10y+9/100+1/100) =10(y-3/10)2+1/10 Vi 10(y-3/10)2>=0 nen 10(y-3/10)2+1/10>=1/10
vay min A=1/10

=x^2-6x+9+4y^2-8y+4+2010
=(x-3)^2+(2y-2)^2+2010>=2010
Dấu = xảy ra khi x=3 và y=1
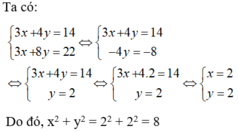
 Đúng thì like giúp mik nha bạn. Thx bạn
Đúng thì like giúp mik nha bạn. Thx bạn
Ta có : \(3x-8y=1\Rightarrow x=\dfrac{8y+1}{3}\)
\(\Rightarrow P=\dfrac{\left(8y+1\right)^2}{9}+y^2=\dfrac{64y^2+16y+1+9y^2}{9}=\dfrac{73y^2+16y+1}{9}\)
\(=\dfrac{73\left(y^2+\dfrac{16}{73}y+\dfrac{1}{73}\right)}{9}=\dfrac{73\left[\left(y^2+\dfrac{16}{73}y+\dfrac{64}{5329}\right)+\dfrac{9}{5329}\right]}{9}\)
\(=\dfrac{73\left[\left(y+\dfrac{8}{73}\right)^2+\dfrac{9}{5329}\right]}{9}\ge\dfrac{73.\dfrac{9}{5329}}{9}=\dfrac{1}{73}\)
Vậy \(MIN_P=\dfrac{1}{73}\) . Dấu \("="\) xảy ra khi \(x=\dfrac{3}{73}\) và \(y=-\dfrac{8}{73}\)