Hai xe chuyển động nhanh dần đều trên cùng một đoạn đường AB để đi đến gặp nhau. Gia tốc của hai xe đều có độ lớn là 0,4 m/s2. Tại thời điểm ta bắt đầu quan sát (t=0) thì xe thứ nhất ở vị trí A, có vận tốc 2 m/s và đang chuyển động đến B; xe thứ hai ở vị trị B cách A 160m và đang có vận tốc là 10 m/s, hướng từ B đến A.
a) Viết phương trình chuyển động của mỗi xe. Chọn gốc tọa độ tại A, chiều dương từ A đến B, gốc thời gian là lúc bắt đầu quan sát ?
b) Sau bao lâu thì 2 xe gặp nhau ?. Xác định vị trí 2 xe gặp nhau ?.

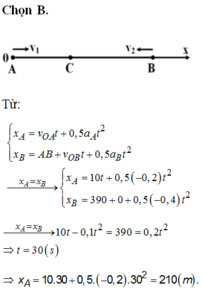

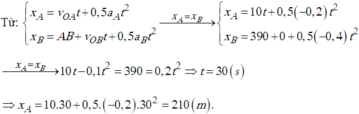


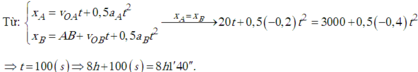



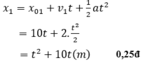
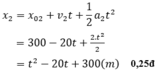
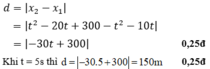
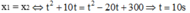 (0,25đ)
(0,25đ)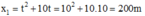 (0,25đ)
(0,25đ)
a) chọn gốc tọa độ tại A
chiều dương tử A đến B, gốc thời gian là lúc bắt đầu quan sát
Phương trình chuển động: \(x=x_0+v_0t+\dfrac{1}{2}at^2\)
xe đi từ A: \(x_A=2t+0,2t^2\)
xe đi từ B : \(x_B=160-10t-0,2t^2\)
b) hai xe gặp nhau khi \(2t+0,2t^2=160-10t-0,2t^2\)
=> t= 10 s)
2 xe gặp nhau cách A : 2.10+0,2.102=40m