Vẽ đồ thị hàm số và nêu cách vẽ biết
y=\(\sqrt{8}\)x
y=\(\sqrt{11}\)x
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 4 2017
Bài giải:
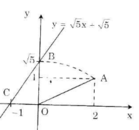
Hình bên diễn tả cách dựng đoạn thẳng có độ dài bằng √5.
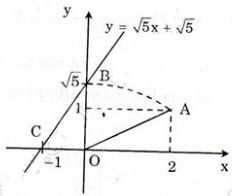
Đồ thị hàm số y = √5 x + √5 đi qua hai điểm A(0; √5) và B(-1; 0).
CM
6 tháng 12 2017
Cho x = 0 => y = √3 ta được (0; √3).
Cho y = 0 => √3 x + √3 = 0 => x = -1 ta được (-1; 0).
Như vậy để vẽ được đồ thị hàm số y = √3 x + √3 ta phải xác định được điểm √3 trên Oy.
Các bước vẽ đồ thị y = √3 x + √3 :
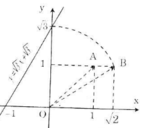
+ Dựng điểm A(1; 1) được OA = √2.
+ Dựng điểm biểu diễn √2 trên Ox: Quay một cung tâm O, bán kính OA cắt tia Ox, được điểm biểu diễn √2.
+ Dựng điểm B(√2; 1) được OB = √3.
+ Dựng điểm biểu diễn √2. Trên trục Oy: Quay một cung tâm O, bán kính OB cắt tia Oy, được điểm biểu diễn √3
+ Vẽ đường thẳng qua điểm biểu diễn √3 trên Oy và điểm biểu diễn -1 trên Ox ta được đồ thị hàm số y = √3 x + √3.
b) Áp dụng vẽ đồ thị hàm số y = √5 x + √5
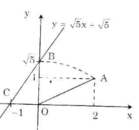
- Cho x = 0 => y = √5 ta được (0; √5).
- Cho y = 0 => √5 x + √5 = 0 => x = -1 ta được (-1; 0).
Ta phải tìm điểm trên trục tung có tung độ bằng √5.
Cách vẽ:
+ Dựng điểm A(2; 1) ta được OA = √5.
+ Dựng điểm biểu diễn √5 trên trục Oy. Quay một cung tâm O, bán kính OA cắt tia Oy, được điểm biểu diễn √5. Vẽ đường thẳng qua điểm biểu diễn √5 trên Oy và điểm biểu diễn -1 trên Ox ta được đồ thị hàm số y = √5 x + √5.
CM
25 tháng 6 2019
a) Cho x = 0 => y = √3 ta được (0; √3).
Cho y = 0 => √3 x + √3 = 0 => x = -1 ta được (-1; 0).
Như vậy để vẽ được đồ thị hàm số y = √3 x + √3 ta phải xác định được điểm √3 trên Oy.
Các bước vẽ đồ thị y = √3 x + √3 :
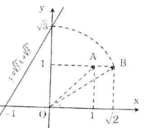
+ Dựng điểm A(1; 1) được OA = √2.
+ Dựng điểm biểu diễn √2 trên Ox: Quay một cung tâm O, bán kính OA cắt tia Ox, được điểm biểu diễn √2.
+ Dựng điểm B(√2; 1) được OB = √3.
+ Dựng điểm biểu diễn √2. Trên trục Oy: Quay một cung tâm O, bán kính OB cắt tia Oy, được điểm biểu diễn √3
+ Vẽ đường thẳng qua điểm biểu diễn √3 trên Oy và điểm biểu diễn -1 trên Ox ta được đồ thị hàm số y = √3 x + √3.
b) Áp dụng vẽ đồ thị hàm số y = √5 x + √5
- Cho x = 0 => y = √5 ta được (0; √5).
- Cho y = 0 => √5 x + √5 = 0 => x = -1 ta được (-1; 0).
Ta phải tìm điểm trên trục tung có tung độ bằng √5.
Cách vẽ:
+ Dựng điểm A(2; 1) ta được OA = √5.
+ Dựng điểm biểu diễn √5 trên trục Oy. Quay một cung tâm O, bán kính OA cắt tia Oy, được điểm biểu diễn √5. Vẽ đường thẳng qua điểm biểu diễn √5 trên Oy và điểm biểu diễn -1 trên Ox ta được đồ thị hàm số y = √5 x + √5.
I
0
10 tháng 4 2021
Câu 1:
1: Ta có: \(16\sqrt{9}-9\sqrt{16}\)
\(=16\cdot3-9\cdot4\)
\(=48-36=12\)
10 tháng 4 2021
2:
a) Thay x=2 và y=8 vào hàm số \(y=a\cdot x^2\), ta được:
\(a\cdot2^2=8\)
\(\Leftrightarrow4a=8\)
hay a=2
Vậy: a=2
AH
Akai Haruma
Giáo viên
22 tháng 7 2021
Lời giải:
a. Hình vẽ:
b. Vì điểm $A$ thuộc đths nên $A$ có tọa độ $(a,3a)$
$OA=\sqrt{a^2+(3a)^2}=2\sqrt{10}$
$\sqrt{10a^2}=2\sqrt{10}$
$10a^2=400$
$a=\pm 2$
Vậy tọa độ điểm A là $(2,6)$ hoặc $(-2,-6)$
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 7 2021
\(y=\left|x+1\right|+\sqrt{\left(x-2\right)^2}=\left|x+1\right|+\left|x-2\right|\)
\(\Rightarrow\left\{{}\begin{matrix}y=2x-1\text{ với }x\ge2\\y=1-2x\text{ với }x\le-1\\y=3\text{ với }-1\le x\le2\end{matrix}\right.\)
Từ đó ta có đồ thị hàm số như sau (vẽ 3 đồ thị hàm bậc nhất xác định trên trên ở từng khoảng của chúng)
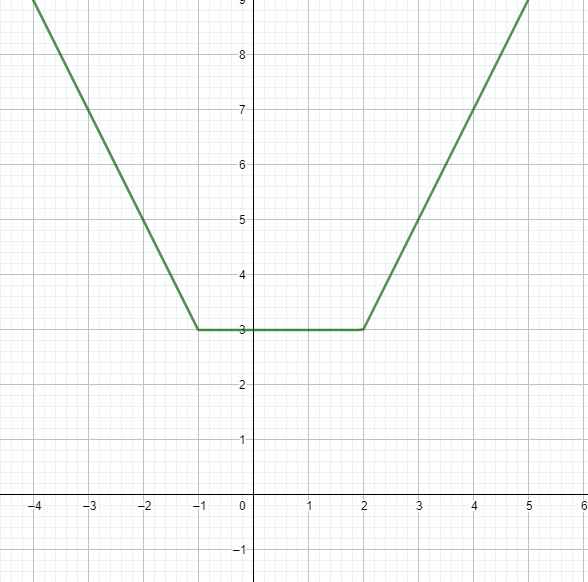
Từ đồ thị \(\Rightarrow y_{min}=3\) khi \(-1\le x\le2\)
25 tháng 12 2023
Bài 3:
\(A=\dfrac{2\sqrt{x}-4}{3\sqrt{x}-4}+\dfrac{x+22\sqrt{x}-32}{3x-10\sqrt{x}+8}+\dfrac{4+2\sqrt{x}}{\sqrt{x}-2}\)
\(=\dfrac{2\sqrt{x}-4}{3\sqrt{x}-4}+\dfrac{x+22\sqrt{x}-32}{\left(3\sqrt{x}-4\right)\left(\sqrt{x}-2\right)}+\dfrac{2\sqrt{x}+4}{\sqrt{x}-2}\)
\(=\dfrac{\left(2\sqrt{x}-4\right)\left(\sqrt{x}-2\right)+x+22\sqrt{x}-32+\left(2\sqrt{x}+4\right)\left(3\sqrt{x}-4\right)}{\left(3\sqrt{x}-4\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{2x-8\sqrt{x}+8+x+22\sqrt{x}-32+6x-8\sqrt{x}+12\sqrt{x}-16}{\left(3\sqrt{x}-4\right)\cdot\left(\sqrt{x}-2\right)}\)
\(=\dfrac{9x+18\sqrt{x}-40}{\left(3\sqrt{x}-4\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{9x-12\sqrt{x}+30\sqrt{x}-40}{\left(3\sqrt{x}-4\right)\left(\sqrt{x}-2\right)}=\dfrac{\left(3\sqrt{x}-4\right)\left(3\sqrt{x}+10\right)}{\left(3\sqrt{x}-4\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{3\sqrt{x}+10}{\sqrt{x}-2}\)
Bài 2:
b: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\-\dfrac{1}{2}x+\dfrac{3}{2}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\3-x=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=3\\y=0\end{matrix}\right.\)
=>A(3;0)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=-\dfrac{1}{2}x+\dfrac{3}{2}=-\dfrac{1}{2}\cdot0+\dfrac{3}{2}=1,5\end{matrix}\right.\)
=>B(0;1,5)
\(OA=\sqrt{\left(3-0\right)^2+\left(0-0\right)^2}=\sqrt{3^2+0^2}=3\)
\(OB=\sqrt{\left(0-0\right)^2+\left(1,5-0\right)^2}=1,5\)
Ox\(\perp\)Oy nên OA\(\perp\)OB
=>ΔOAB vuông tại O
=>\(S_{OAB}=\dfrac{1}{2}\cdot OA\cdot OB=2.25\)
Bài 1:
a: ĐKXĐ: \(x\in R\)
\(\sqrt{x^2+4x+4}=2\)
=>\(\sqrt{\left(x+2\right)^2}=2\)
=>|x+2|=2
=>\(\left[{}\begin{matrix}x+2=2\\x+2=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-4\end{matrix}\right.\)
b: ĐKXĐ: x>=2
\(\sqrt{4x-8}-7\cdot\sqrt{\dfrac{x-2}{49}}=5\)
=>\(2\sqrt{x-2}-7\cdot\dfrac{\sqrt{x-2}}{7}=5\)
=>\(\sqrt{x-2}=5\)
=>x-2=25
=>x=27(nhận)
mình biết nội quy rồi nên đưng đăng nội quy
ai chơi bang bang 2 kết bạn với mình
mình có nick có 54k vàng đang góp mua pika
ai kết bạn mình cho