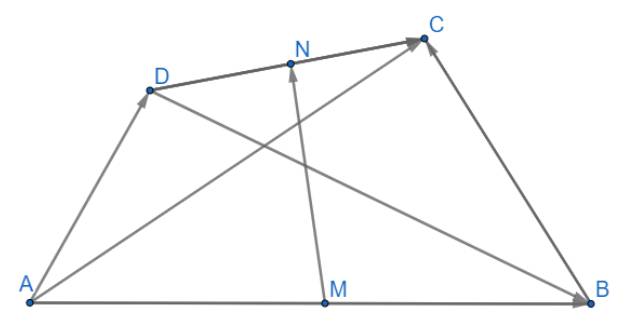
Cho hình bình hành ABCD. Trên BD lấy các điểm G và H sao cho \(DG=GH=HB\)
a) Chứng minh \(\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AG}+\overrightarrow{AH}\).
b) Giả sử AH cắt Bc tại M, AG cắt CD tại N. Chứng minh: \(\overrightarrow{AM}+\overrightarrow{AN}=\dfrac{3}{2}\overrightarrow{AC}\)

a: vecto AB+vecto AC
=vecto AB+vecto AB+vecto AD
=2 vecto AB+vecto AD
=2(vecto AH+vecto HB)+vecto AG+vecto GD
=2vecto AH+2 vecto HB+vecto AG+vecto GD
=2 vecto AH+vecto AG+vecto GB+vecto GD
=2 vecto AH+vecto AG
b: Xét tứ giác AHCG có
O là trung điểm chung của CA và HG
nên AHCG là hình bình hành
Suy ra: AH//CG
Xét ΔDHC có
G là trung điểm cua rDH
GN//HC
Do đó: N là trung điểm của DC
Xét ΔBGC có
H là trung điểm của BG
HM//GC
Do đó: M là trung điểm của BC
\(\overrightarrow{AM}+\overrightarrow{AN}\)
\(=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{AC}\)
=3/2 vecto AC