Cho hình chữ nhật có hai cạnh là 3 và căn 3. Tính các góc tạo bởi cạnh và đường chéo.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi O là giao điểm của hai đường chéo AC và BD.
AC = BD (tính chất hình chữ nhật)
\(\Rightarrow OA=OD=\dfrac{1}{2}AC\)
\(AD=\dfrac{1}{2}AC\left(gt\right)\)
\(\Rightarrow OA=OD=AD\)
\(\Rightarrow\Delta OAD\) đều
\(\Rightarrow\widehat{AOD}=60^0\)

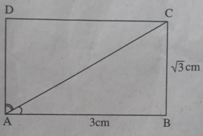
Hình chữ nhật ABCD có AB = 3cm, BC = 3 cm nên
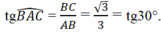
Vậy ∠ (BAC) = 30 °
∠ (DAC) = 90 ° - 30 ° = 60 °

B.Hình vuông có tất cả các tính chất của hình chữ nhật và hình thoi

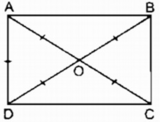
Gọi O là giao điểm của hai đường chéo AC và BD.
Ta có: AC = BD ( tính chất hình chữ nhật) ⇒ OA = OD = 1/2 AC
Lại có: AD = 1/2 AC (gt)
Suy ra: OA = OD = AD
⇒ ∆ OAD đều ⇒ ∠ (AOD ) = 60 0

1) Đỉnh: A, B, C, D
Cạnh: AB, BC, CD, DA
Đường chéo: AC, BD
Hai cạnh đối: AB và CD; BC và AD
2) Ta đo được: \(\widehat{A} = 90^0; \widehat{B} = 90^0; \widehat{C} = 90^0; \widehat{D} = 90^0\). Vậy các góc của hình chữ nhật đều bằng nhau và bằng 90o
3) Ta đo được: AB = CD ; AD = BC nên hai cạnh đối của hình chữ nhật bằng nhau
AC = BD nên hai đường chéo của hình chữ nhật bằng nhau.