giúp mình câu b và c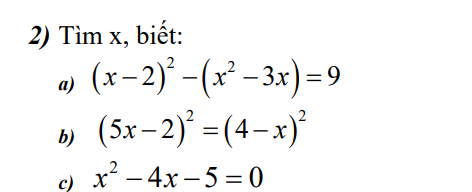
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bạn có thể cho mình hỏi vì sao góc HDC + góc ABC = 90 độ đc không?



a: Xét (O) có
ΔCNM nội tiếp
CM là đường kính
Do đó: ΔCNM vuông tại N
=>CN\(\perp\)NM tại N
=>CN\(\perp\)NB tại N
Xét tứ giác ABCN có \(\widehat{CAB}=\widehat{CNB}=90^0\)
nên ABCN là tứ giác nội tiếp
b: Xét (O) có
ΔCEM nội tiếp
CM là đường kính
Do đó: ΔCEM vuông tại E
Xét ΔCEM vuông tại E và ΔCAB vuông tại A có
\(\widehat{ECM}\) chung
Do đó: ΔCEM~ΔCAB
=>\(\dfrac{CE}{CA}=\dfrac{CM}{CB}\)
=>\(CE\cdot CB=CA\cdot CM\)
c: Xét (O) có
\(\widehat{DNM}\) là góc nội tiếp chắn cung DM
\(\widehat{DCM}\) là góc nội tiếp chắn cung DM
Do đó: \(\widehat{DNM}=\widehat{DCM}\)
=>\(\widehat{DNM}=\widehat{DCA}\)
mà \(\widehat{ACB}=\widehat{DNM}\)(ABCN là tứ giác nội tiếp)
nên \(\widehat{DCA}=\widehat{ACB}\)
=>CA là phân giác của góc BCD




\(a,C=\dfrac{81-1}{4\cdot9}=\dfrac{80}{36}=\dfrac{20}{9}\\ b,D=\dfrac{x+2\sqrt{x}+1+x-\sqrt{x}+\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ D=\dfrac{2x+2\sqrt{x}+1}{x-1}\\ c,CD=\dfrac{x-1}{4\sqrt{x}}\cdot\dfrac{2x+2\sqrt{x}+1}{x-1}=\dfrac{2x+2\sqrt{x}+1}{4\sqrt{x}}=\dfrac{13}{8}\\ \Leftrightarrow52\sqrt{x}=16x+16\sqrt{x}+8\\ \Leftrightarrow16x-36\sqrt{x}+8=0\\ \Leftrightarrow4x-9\sqrt{x}+2=0\\ \Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=2\\\sqrt{x}=\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\left(tm\right)\\x=\dfrac{1}{16}\left(tm\right)\end{matrix}\right.\)
\(d,N=CD=\dfrac{2x+2\sqrt{x}+1}{4\sqrt{x}}=\dfrac{\sqrt{x}}{2}+\dfrac{1}{2}+\dfrac{1}{4\sqrt{x}}\\ \Leftrightarrow N\ge2\sqrt{\dfrac{\sqrt{x}}{2}\cdot\dfrac{1}{4\sqrt{x}}}+\dfrac{1}{2}=2\sqrt{\dfrac{1}{8}}+\dfrac{1}{2}=\dfrac{\sqrt{2}+1}{2}\)
Dấu \("="\Leftrightarrow4x=2\Leftrightarrow x=\dfrac{1}{2}\left(tm\right)\)
Vậy \(N_{min}=\dfrac{\sqrt{2}+1}{2}\)
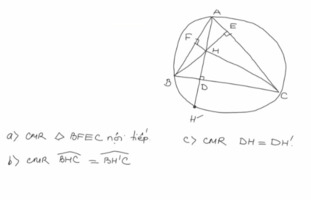
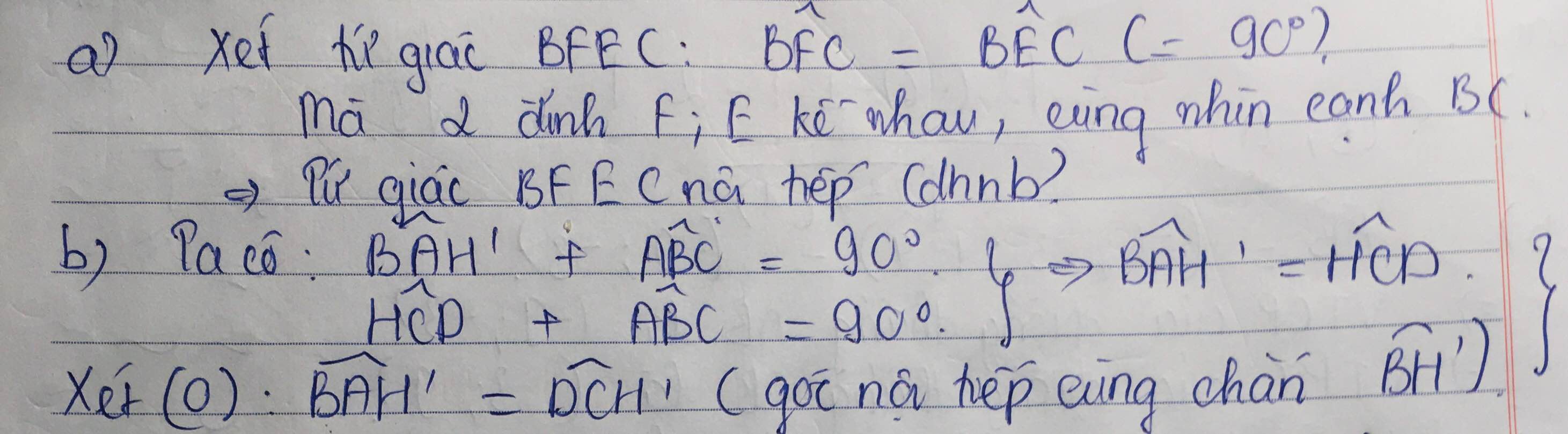


 mình xin lỗi vì ảnh kia bị lỗi. Giúp mình câu a,b,c,d nha còn biểu đồ mình đã làm câu 1.4 và 2.4 r nên mn giúp mình các câu còn lại nhé. Cám ơn
mình xin lỗi vì ảnh kia bị lỗi. Giúp mình câu a,b,c,d nha còn biểu đồ mình đã làm câu 1.4 và 2.4 r nên mn giúp mình các câu còn lại nhé. Cám ơn



 vẽ giúp mình hình và câu c,b với ạ, mình cảm ơn
vẽ giúp mình hình và câu c,b với ạ, mình cảm ơn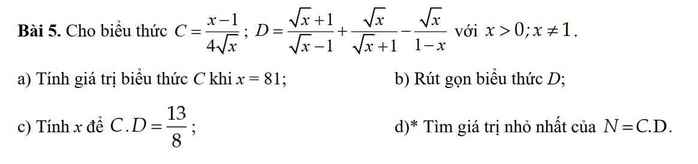
mình làm cho bạn rồi mà