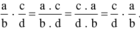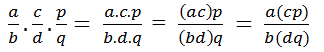Chứng minh tính chất giao hoán, tính chất kết hợp và tính chất của vecto-không
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 4 2019
Ta đã biết tính chất kết hợp của phép nhân là:
(a.b).c = a.(b.c)
Từ đó ta có:
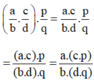
(áp dụng tính chất kết hợp của số nguyên cho cả tử và mẫu)
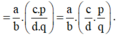
Vậy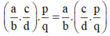 
(tính chất kết hợp của phép nhân phân số)
28 tháng 3 2018
(ab.cd).pq=a.cb.d.pq=(a.c).p(b.d).q(ab.cd).pq=a.cb.d.pq=(a.c).p(b.d).q
ab.(cd.pq)=ab.c.pd.q=a.(c.p)b.(d.q)ab.(cd.pq)=ab.c.pd.q=a.(c.p)b.(d.q)
Theo tính chất kết hợp của phép nhân các số nguyên ta có:
(a.c).p = a.(c.p) và b. (d.q) = (b. d) . q.
Do đó: (ab.cd).pq=ab.(cd.pq)
H
7 tháng 9 2018
VD: - Tính chất giao hoán của phép cộng: 1 + 2 = 2 +1
- Tính chất kết hợp của phép cộng: 1 + 2 + 8 = 1 + (2+8)
- Tính chất giao hoán của phép nhân: 1.2 = 2.1
- Tính chất kết hợp của phép nhâ: 2.45.50 = (2.50).45
17 tháng 4 2017
Ta đã biết tính chất kết hợp của phép nhân là:
(a.b).c = a.(b.c)
Từ đó ta suy ra tính chất kết hợp của phép nhân phân số:
17 tháng 4 2017
Ta đã biết tính chất kết hợp của phép nhân là:
(a.b).c = a.(b.c)
Từ đó ta suy ra tính chất kết hợp của phép nhân phân số: